Distances et tangente

Distances et tangente
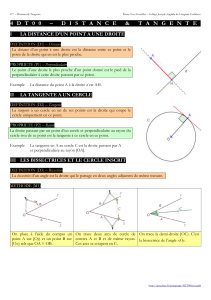
I) Distance d’un point à une droite :
a) Définition :
Définition :
Soit (d) une droite et A un point n’appartenant pas à (d).
La distance du point A à la droite (d) est la longueur AH où H désigne le
point d’intersection de la droite (d) avec la perpendiculaire à la droite (d)
passant par A.
Remarque :
La distance AH est la plus courte distance entre le point A et tous les points de la droite
(d).
Exemple :
Soit (d) une droite et A un point n’appartenant pas à (d). Voici la méthode pour
déterminer la distance du point A à cette droite.
Première étape : On trace la perpendiculaire à la droite (d) passant par A. Elle coupe
(d) en H.

Deuxième étape : On mesure la longueur AH qui correspond à la distance entre le point
A et la droite (d).
On trouve ici AH = ……
b) Propriété :
Propriété :
L’ensemble des points situés à une même distance d’une droite (d) est défini par
deux droites parallèles à (d) situées de part et d’autre de (d).
Exemple :
Soit (d) une droite. Construire en rouge l’ensemble des points situés à 3 cm de la droite
(d).
Voici la méthode :
Première étape :
On trace une droite (d’) perpendiculaire à la droite (d) qu’elle coupe en H. Sur cette
droite (d’) on place deux points M et M’ situés de part et d’autre de la droite (d) à 3 cm
du point H.

Deuxième étape :
On trace les parallèles à la droite (d) passant par M et M’. L’ensemble recherché est
constitué par ces deux droites.
II) Tangente à un cercle en un point :
Définition :
La tangente à un cercle (C) de centre O en un point A est la droite passant
par A et perpendiculaire au rayon [OA].
Exemple :
Construire la tangente au point A au cercle (C) de centre O.
Voici la méthode :

Première étape :
On trace le cercle de centre O, on place le point A et on trace le rayon [OA].
Deuxième étape :
On trace la droite (d) passant par A et perpendiculaire à la droite (OA).
La droite (d) est la tangente en A au cercle (C).
III) Bissectrice d’un angle et cercle inscrit :
Propriété :
• Si un point est situé à la même distance des côtés d’un angle alors il appartient à
la bissectrice de cet angle.
• Réciproquement, si un point appartient à la bissectrice d’un angle alors il est situé
à la même distance des côtés de cet angle.

Exemple n°1 :
On sait que le point M est situé à égales
distantes des côtés de l’angle BÂC.
On en déduit que le point M appartient
à la bissectrice de l’angle BÂC.
Exemple n°2 :
On sait que le point M appartient à la
bissectrice de l’angle BÂC.
On en déduit que le point M est situé à
égales distances des côtés de l’angle
BÂC.