Recherche d`arbres couvrants complètement indépendants

Recherche d’arbres couvrants compl`etement
ind´ependants dans des graphes r´eguliers
Nicolas Gastineau, Benoit Darties, Olivier Togni
To cite this version:
Nicolas Gastineau, Benoit Darties, Olivier Togni. Recherche d’arbres couvrants compl`etement
ind´ependants dans des graphes r´eguliers. ALGOTEL 2014 – 16`emes Rencontres Franco-
phones sur les Aspects Algorithmiques des T´el´ecommunications, Jun 2014, Le Bois-Plage-en-R´e,
France. pp.1–4, 2014. <hal-00986223>
HAL Id: hal-00986223
https://hal.archives-ouvertes.fr/hal-00986223
Submitted on 1 May 2014
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

Recherche d’arbres couvrants complètement
indépendants dans des graphes réguliers
Nicolas Gastineau12, Benoît Darties1and Olivier Togni1
1LE2I, UMR CNRS 6306, Université de Bourgogne, 9 Rue Alain Savary, 21 000 Dijon, France
2LIRIS, UMR CNRS 5205, Université Claude Bernard Lyon 1, Villeurbanne, France
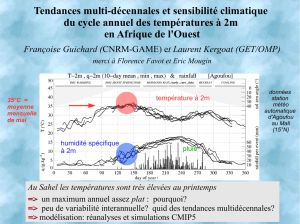
Nous étudions l’existence de rarbres couvrants complètement indépendants dans des graphes 2r-réguliers et 2r-
connexes, et énonçons des conditions nécessaires à leur existence. Nous déterminons le nombre maximum d’arbres
dans les produits cartésiens d’une clique et d’un cycle. Nous montrons que ce nombre n’est pas toujours r.
1 Introduction
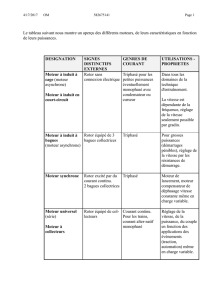
Les arbres couvrants sont une structure fortement utilisée dans de nombreuses opérations réseau (proto-
coles de routage, mécanismes d’évitement de boucles de niveau 2, . . .). La notion d’arbres couvrants com-
plètement indépendants (CIST-Completely Independent Spanning Trees) a été introduite par T. Hasunuma
[1] en complément aux travaux antérieurs sur les arbres couvrants indépendants, et trouve de nombreuses
applications dans des problèmes de répartition de charge du trafic de diffusion ou encore de robustesse
face aux pannes. Soit Gun graphe non orienté représentant un réseau avec V(G)l’ensemble de ses nœuds
et E(G)celui de ses liens directs. Deux chemins P1et P2entre deux sommets xet ydans Gsont dits
sommets-disjoints ssi ils ne partagent aucun sommet entre eux, exception faite de leurs extrémités, i.e.
V(P1)∩V(P2) = {x,y}. Soit un ensemble T1,...,Trde r≥2 arbres couvrants de G, on note E(Ti)les liens
de Tiet PTi(x,y)l’unique chemin reliant xàydans Ti, pour tout i|1≤i≤ret tout x,y∈V(G). Alors les
arbres de cet ensemble sont dits complètement indépendants ssi pour tout i|1≤i≤r, et tout j|1≤j≤r
avec i6=j, les deux conditions suivantes sont réunies :
—Tiet Tjne partagent aucune arête en commun (cad. E(Ti)∩E(Tj) = / 0) ;
— pour tout x,y∈V(G), les chemins PTi(x,y)et PTj(x,y)dans Tiet Tjsont sommet-disjoints.
Une définition équivalente [1] veut que T1,...,Trsoit un ensemble de rarbres couvrants complètement
indépendants ssi aucun arbre ne partage d’arête commune, et que tout nœud interne de l’un soit feuille dans
les r−1 autres. Les arbres couvrants complètement indépendants ont été étudiés pour certaines classes
de graphes, comme les graphes représentatifs des arêtes de graphes[1], les graphes planaires maximaux
[2], très récemment sur les produits cartésiens de deux cycles ou grilles toriques [3], ainsi que les graphes
complets, les graphes complets bipartis et tripartis [4]. Le problème de décision consistant à déterminer
l’existence de deux CIST sur un graphe Gest NP-Complet [2].
Nous nous intéressons à l’existence de rCIST sur les graphes k-réguliers (tous les sommets ont le même
degré k). Il a été conjecturé que pour tout graphe 2r-connexe, il existe rCIST[2]. Un contre-exemple donné
dans [5] réfute cette conjecture, mais n’est pas un graphe régulier. Nous proposons d’étudier cette conjec-
ture pour les graphes 2r-connexes et 2r-réguliers. Dans la suite, nous présentons d’abord les conditions
nécessaires à l’existence de rCIST sur les graphes 2r-réguliers. Nous déterminons ensuite une classe de
graphes à la fois 2r-réguliers et 2r-connexes pour lesquels il n’existe pas toujours rCIST. Nous étendons
enfin nos résultats et résolvons le problème du nombre maximum de CIST pour cette classe donnée.
2 Conditions nécessaires sur les graphes 2r-réguliers
Dans cette section, nous considérons un graphe 2r-régulier Gd’ordre n, et supposons qu’il existe un
ensemble {T1,...,Tr}de rCIST. Les propositions énoncées ici s’appliquent sur cette configuration unique-

N. Gastineau, B. Darties, O. Togni
ment. Nous notons dH(u)le degré de udans le graphe H, le graphe Hétant possiblement un sous-graphe
d’un autre graphe. Nous notons in(Ti)l’ensemble des nœuds internes de l’arbre Ti, et lea f (Ti)l’ensemble
de ses feuilles (sommets de degré 1). Pour rappel, in(Ti)∩in(Tj) = / 0|i6=j,1≤i≤r,1≤j≤r. Tout nœud
xest feuille d’au moins r−1 arbres, et de degré 2rdans G. Nous avons :
Proposition 1. S’il existe un ensemble {T1,...,Tr}de r CIST, tout nœud interne de tout arbre Tia un degré
d’au plus r +1dans Ti.
Un sommet étant nœud interne d’au plus un arbre, nous avons naturellement ∑r
i=1|in(Ti)| ≤ n. Soit min
l’indice de l’arbre ayant le plus petit nombre de nœuds internes, cad. in(Tmin)≤ |in(Ti)|pour tout i6=min .
Proposition 2. S’il existe un ensemble {T1,...,Tr}de r CIST, alors |in(Tmin)| ≤ ⌊n/r⌋.
Démonstration. Par l’absurde. Si |in(Ti)| ≥ ⌊n/r⌋+1 pour tout i, alors ∑r
i=1|in(Ti)| ≥ ⌊n/r⌋r+r>n
Proposition 3. S’il existe un ensemble {T1,...,Tr}de r CIST, alors pour tout i, 1≤i≤r, on a
n−2
r≤ |in(Ti)| ≤ n−n−2 r(r−1)(1)
Démonstration. Rappelons que pour tout arbre Ti,∑
v∈V(Ti)
dTi(v) = ∑
v∈in(Ti)
dTi(v) + ∑
v∈lea f (Ti)
dTi(v) = 2(n−1).
Puisque |in(Ti)|+|lea f (Ti)|=n, et que dTi(v)≤r+1 pour tout v∈in(Ti)(d’après la proposition 1), nous
obtenons 2(n−1) = ∑
v∈V(T)
d(v)≤ |in(Ti)|(r+1)+|lea f (Ti)|=|in(Ti)|r+n, et finalement ⌈n−2
r⌉ ≤ |in(Ti)|.
Depuis l’inégalité ∑r
i=1|in(Ti)| ≤ n, nous pouvons écrire in(Ti)≤n−∑r
j=1,i6=j|in(Tj)|. En reprenant l’in-
égalité ⌈n−2
r⌉ ≤ |in(Ti)|précédemment montrée, nous obtenons in(Ti)≤n− ⌈ n−2 r⌉(r−1).
Pour un ensemble de rCIST, appelons EP=E(G)− ∪1≤i≤rE(Ti)l’ensemble des arêtes perdues, cad. qui
n’appartiennent à aucun arbre. Puisque Gest 2r-régulier, donc que |E(G)|=rn, et que chacun des rarbres
contient (n−1)arêtes, alors on a |EP|=r. Pour chaque arbre Tinous appelons EP
iles arêtes de EPdont les
2 extrémités appartiennent à in(Ti). Puisque ∪1≤i≤rEP
i⊆EP, alors on a ∑r
i=1|EP
i| ≤ r.
Tout arbre couvrant de in(T)nœuds internes possède au maximum in(T)(r−1) + 2 feuilles. Supposons
un arbre couvrant idéal T∗dont les nœuds internes in(T∗)sont tous de degré (r+1). La somme des degrés
de ses nœuds peut s’écrire |in(T∗)|(r+1) + (n− |in(T∗)|) = |in(T∗)|r+n.
Definition 1. Nous appelons potentiel extra-degré d’un arbre couvrant T le nombre de feuilles qu’il aurait
pu posséder en plus si tous ses nœuds internes étaient de degré r +1, et le notons ped(T). Formellement,
ped(T)est la différence entre la somme des degrés d’un arbre idéal de in(T)nœuds internes et la somme
des degrés de T , soit ped(T) = |in(T)|r+n−2(n−1) = |in(T)|r−n+2.
Pour un arbre couvrant idéal T∗, on a ped(T∗) = 0. Autrement, ped(T)>0 et le nombre de nœuds
internes de degré strictement inférieur à r+1 est borné par ped(T). Remarquons que toute arête perdue
e∈EP
iayant ses 2 extrémités dans in(Ti)mais n’appartenant pas à Tiaugmente ped(Ti)de 2 unités :
chacune de ses extrémité doit être incidente à eet adjacente à r−1 nœuds internes de chacun des autres
arbres dont elle est feuille. Le degré des extrémités de edans Tine peut donc excéder r. En conséquence :
Proposition 4. S’il existe un ensemble {T1,...,Tr}de r CIST sur un graphe 2r-régulier :
1. La somme ∑r
i=1ped(Ti)ne peut excéder 2 fois le nombre d’arêtes perdues EP:∑r
i=1ped(Ti)≤2r.
2. Pour tout i, 1≤i≤r, on a 2|EP
i| ≤ ped(Ti).
3 Application sur le produit cartésien d’une clique et d’un cycle
Pour deux graphes Get H, le produit cartésien de Get H, noté GH, est le graphe ayant pour sommets
V(G)×V(H)et pour arêtes {(u,u′)(v,v′)|(u=v∧u′v′∈E(H))∨(u′=v′∧uv ∈E(G))}. Soient deux entiers
m>1 et ℓ > 2 , dans cette section le graphe considéré est KmCℓ, où Kmest une clique d’ordre met Cℓun
cycle d’ordre ℓ, et possède mℓsommets.
Ce graphe peut être construit en considérant une clique originale K0de msommets {u0
0,...,u0
m−1}que
l’on aurait dupliqué ℓ−1 fois en cliques notées K1,...,Kℓ−1, et en notant {ui
0,...,ui m−1}les sommets de la

Recherche d’arbres couvrants complètement indépendants dans des graphes réguliers
clique Ki. Chaque sommet ui
jest ensuite connecté à son sommet clone dans la clique d’indice immédiate-
ment supérieur, à savoir ui+1(mod ℓ)
j, pour tout tout i, 0 ≤i≤ℓ−1, et tout j, 0 ≤j≤m−1. Nous réutilisons
cette dénomination des sommets dans la suite. Le graphe KmCℓest clairement (m+1)-régulier et (m+1)-
connexe. Deux cliques d’indices consécutifs sont dites adjacentes. Chaque sommet ui
jd’une clique Kiest
incident à exactement un sommet ui−1
j(resp. ui+1 j) de la clique d’indice immédiatement inférieur (resp.
supérieur). Les indices id’une clique Kiou d’un sommet ui
jsont toukours supposés modulo ℓdans la suite.
Notre objectif est de montrer qu’il n’existe pas d’ensemble de rCIST dans K2r−1Cℓpour certaines
valeurs de ret ℓ. Pour cela, nous supposons l’existence d’un ensemble de rCIST, et montrons qu’il contredit
les propositions énoncées dans les sections précédentes et courantes.
Nous considérons le graphe K2r−1Cℓet posons n=|V(K2r−1Cℓ)|=ℓ(2r−1)son nombre de sommets.
Nous supposons l’existence d’un ensemble {T1,...,Tr}de rCIST sur ce dernier. Soit Tmin l’arbre ayant le
plus petit nombre de nœuds internes. D’après la proposition 2, puisque n=ℓ(2r−1)nous avons :
|in(Tmin)| ≤ ⌊n/r⌋=2ℓ− ⌈ℓ/r⌉(2)
Puisque ped(Tmin) = |in(Tmin)|r−n+2, combiné à l’équation 2, nous obtenons :
ped(Tmin) = |in(Tmin)|r−n+2≤ −⌈ℓ/r⌉r+ℓ+2≤2 (3)
L’arbre Tmin satisfait ped(Tmin) = 2 si et seulement si ℓ≡0(mod r), et ped(Tmin)≤1 autrement.
Dans la suite, nous regardons la répartition des sommets internes de Tmin dans les différentes cliques
de K2r−1Cℓet montrons qu’aucune répartition valide n’est possible. Nous appelons V(Ki)∩in(Tmin)l’en-
semble des sommets internes de Tmin qui sont dans la clique Ki. Rappelons que puisque 2|EP
min| ≤ ped(Tmin)
par le point 2 de la proposition 4, et que ped(Tmin)≤2 dans l’équation 3, on a |EP
min| ≤ 1.
Proposition 5. La répartition des nœuds internes de Tmin dans toute clique Ki, avec 1≤i≤ℓest telle que
1. si une clique Kicontient k nœuds internes de Tmin, alors 1
2(k−1)(k−2)arêtes de Kisont dites
perdues, et appartiennent donc à EP
min ;
2. une clique Kine peut contenir un nombre de nœuds internes de Tmin strictement supérieur à 3 :
|V(Ki)∩in(Tmin)| ≤ 3pour tout i tel que 1≤i≤ℓ.
3. il ne peut pas y avoir plus d’une clique contenant 3nœuds internes de Tmin ;
4. s’il existe une clique Kicontenant 3nœuds internes de Tmin, alors l ≡0(mod r)et ℓ≥r ;
5. il existe au moins une clique Kicontenant strictement moins de 2nœuds internes de Tmin ;
6. si pour chaque clique Kion a V (Ki)∩in(Tmin)≥1, alors le nombre de cliques contenant 3nœuds
internes de Tmin est strictement inférieur à celui contenant exactement 1nœud interne de Tmin .
Démonstration. .
(1) : 1
2k(k−1)arêtes lient les knœuds internes de V(Ki)∩in(Tmin)entre eux. Seulement k−1 sont
utilisées dans Tmin. Les autres sont donc des arêtes perdues et ajoutées à EP
min.
(2) et (3) : Conséquence du point (1), autrement nous aurions |EP
min|>1.
(4) : Si |V(Ki)∩in(Tmin)|=3, alors |EP
min| ≥ 1 et donc ped(Tmin)≥2. Réutilisé dans l’inéquation 3, on
obtient −⌈ℓ/r⌉r+ℓ+2=2, et donc ℓ≡0(mod r). Puisque ℓ > 0, on a ℓ≥r.
(5) et (6) : L’équation 2 dit que le nombre de nœuds internes de Tmin est strictement inférieur à deux fois
le nombre de cliques. Posons a,b,cet dle nombre de cliques ayant 0, 1, 2 ou 3 nœuds internes, avec
a+b+c+d=ℓ, il faut que b+2c+3d<2ℓ, donc que a+b>0. Si a=0, il faut que d<b.
Lemme 1. Pour tout ℓ≥2et tout r ≥6, il n’existe pas d’ensemble de r CIST sur K2r−1Cℓ.
Démonstration. Supposons l’existence de rCIST. Soit Tmin l’arbre tel que in(Tmin) = min1≤i≤rin(Ti)
Si une clique Ki, 1 ≤i≤ℓ, ne contenait aucun nœud de in(Tmin), alors connecter les sommets de Kiaux
nœuds internes de Tmin nécessiterait au moins 2r−1≥11 nœuds dans {V(Ki−1)∩in(Tmin)}S{V(Ki+1)∩
in(Tmin)}, d’où |V(Ki−1)∩in(Tmin)| ≥ 6 ou |V(Ki+1)∩in(Tmin)| ≥ 6, et contradiction avec la proposition
5-(2). Soit il’indice d’une clique telle que |V(Ki)∩in(Tmin)|=1 (cet indice existe d’après la proposition 5-
(5)), et appelons ule seul élément de V(Ki)∩in(Tmin). Le nœud uest de degré au plus r+1 dans Tmin et doit

N. Gastineau, B. Darties, O. Togni
être adjacent à au moins un nœud interne vd’une clique incidente Ki−1ou Ki+1. Donc une peut connecter
au mieux que rdes 2r−2 autres sommets de KiàTmin, et restent r−2≥4 nœuds de Kiqui doivent
être incidents à r−2 nœuds de {V(Ki−1)∩in(Tmin)}S{V(Ki+1)∩in(Tmin)}, autres que vqui connecte
déjà u. Alors on a forcément |V(Ki−1)∩in(Tmin)| ≥ 3 ou |V(Ki+1)∩in(Tmin)| ≥ 3. En conséquence, toute
clique Kiavec |V(Ki)∩in(Tmin)|=1 doit être incidente à une clique contenant 3 sommets internes de
Tmin. Or, il faut plus de cliques contenant un seul nœud interne que de cliques en contenant 3, et on ne
peut en avoir plus d’une (propositions 5-(6) et 5-(3)). La seule possibilité est d’avoir une clique Kjde 3
nœuds internes, dont les deux cliques adjacentes Kj−1et Kj+1contiennent chacune un seul nœud interne
de Tmin. Soit x, resp. y, le nœud interne de Kj−1, resp. de Kj+1. D’après la proposition 5-(4), on a au
moins ℓ≥r≥6 cliques. Pour assurer la connexité de Tmin, au moins xou ydoit être adjacent à un nœud
interne de Kj−2ou Kj+2. Supposons qu’il s’agisse de x. Le sommet xne peut connecter au mieux que r−1
sommets feuilles de Kj−1àTmin. Restent r−1≥5 nœuds de Kj−1qui doivent être adjacents à des nœuds
de {V(Kj−2)∩in(Tmin)}S{V(Kj)∩in(Tmin)}, autres que les 2 connectant déjà xà chaque clique voisine.
On a donc forcement, |{V(Kj−2)∩in(Tmin)}S{V(Kj)∩in(Tmin)}| ≥ 7, donc |V(Kj−2)∩in(Tmin)| ≥ 4 ou
|V(Kj)∩in(Tmin)| ≥ 4, mais ceci est en contradiction avec la proposition 5-(2).
En utilisant un raisonnement similaire, nous avons établi les lemmes suivants (preuves non présentées) :
Lemme 2. Pour tout 4≤r≤5et tout ℓ≥r+1, il n’existe pas d’ensemble de r CIST sur K2r−1Cℓ.
Lemme 3. Il n’existe pas d’ensemble de 5CIST sur K9C3.
Nous avons ensuite proposé un programme linéaire en nombres entiers (PLNE) afin de résoudre le pro-
blème pour des valeurs de met ℓfixées. Les résultats suivants montrent que pour certaines valeurs de met
ℓoù K2r−1Cℓest un graphe 2r-connexe et 2r-régulier, on peut quand même trouver rCIST :
Lemme 4. Il existe 5CIST dans K9C4et dans K9C5.
Lemme 5. Il existe 4CIST dans K7C3et dans K7C4.
En couplant les résultats de la PLNE avec une répétition de motifs, nous obtenons la proposition suivante :
Lemme 6. Soit ℓ≥3un entier. Il existe 3CIST dans K5Cℓ.
Appelons Mcist (G)le nombre maximum de CIST pour un graphe Gdonné. En s’appuyant sur les résultats
des différents lemmes, nous avons pu proposer une construction de Mcist (KmCℓ)arbres basés sur des
motifs pour l’ensemble des valeurs de m≥3 et ℓ≥3. Nous revendiquons la véracité du théorème suivant :
Theorem 1. Soient m ≥3et ℓ≥3deux entiers. Nous avons :
Mcist (KmCℓ) = ⌈m/2⌉,si m ∈ {3,5}ou (m =7∧ℓ∈ {3,4}) ou (m =9∧ℓ∈ {4,5}) ;
⌊m/2⌋,autrement.
4 Perspectives
En perspectives, nous souhaitons déterminer les conditions suffisantes pour garantir l’existence de rCIST,
et poursuivre l’étude de ces derniers sur d’autres classes de graphes, comme les hypercubes, . . ..
Références
[1] Toru Hasunuma. Completely independent spanning trees in the underlying graph of line graph. Dis-
crete mathematics, 234 :149–157, 2001.
[2] Toru Hasunuma. Completely independent spanning trees in maximal planar graphs. Lecture Notes in
Computer Science, 2573 :235–245, 2002.
[3] Toru Hasunuma and Chie Morisaka. Completely independent spanning trees in torus networks. Net-
works, 60 :56–69, 2012.
[4] Kung-Jui Pai, Shyue-Ming Tang, Jou-Ming Chang and Jinn-Shyong Yang. Completely Independent
Spanning Trees on Complete Graphs, Complete Bipartite Graphs and Complete Tripartite Graphs.
Advances in Intelligent Systems and Applications - Volume 1, 20 :107–113, 2013.
[5] Ferenc Péterfalvi. Two counterexamples on completely independent spanning trees. EGRES Quick-
Proof, 01, 2011.