Corrigé 1. (0,5 pt) • La première observation montre que

18/04/2013 Corrigé exo 3.doc 1/1
EXERCICE III – LES ONDES SONORES ET L’OREILLE (5 points)
Corrigé
1. (0,5 pt)
 La première observation montre que les ondes sonores sont des ondes mécaniques qui ont besoin d'un
support matériel pour se propager, elles ne se propagent pas dans le vide.
 La seconde observation montre que les ondes sonores sont des ondes longitudinales, la perturbation
étant parallèle au sens de déplacement de l'onde sonore.
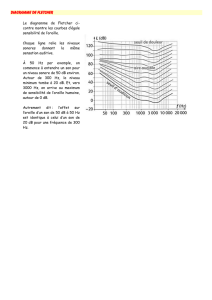
2.1. (0,25 pt) Une courbe isosonique est une courbe qui correspond à un même niveau d'intensité sonore perçu
par l'oreille.
2.2. (0,25 pt) On ne peut pas entendre ce son de 40 Hz à 40 dB car il est en dessous du seuil normal d'audition.
2.3. (0,25 pt) Entre 1kHz et 10 kHz, pour des niveaux sonores entre 20 dB et 80 dB.
2.4. (0,25 pt) Le minimum des courbes de sensibilités est atteint autour de 3000 - 5000 Hz, ce qui correspond au
maximum de sensibilité.
2.5. (0,5 pt) En imaginant par interpolation la courbe d'égale sensation auditive passant par le point de
coordonnées (500 Hz ; 40 dB), on constate que le point d'abscisse 100 Hz a pour ordonnée 55 dB environ.
Un son de fréquence 100 Hz et de niveau d'intensité sonore 55 dB, donne la même sensation auditive qu'un
son de fréquence 500 Hz à 40 dB.
2.6. (0,5 pt) La réponse à la question précédente apporte un élément d'explication :
Pour une fréquence inférieure à 1000 Hz, l'oreille humaine est plus sensible aux sons aigus qu'aux sons
graves. Ainsi, utilisant des sons plus aigus, une publicité paraît plus sonore qu'un documentaire sonore d’égal
niveau sonore mais plus grave. Donc un son de fréquence 500 Hz à 40 dB donne une sensation auditive
supérieure à un son de fréquence 100 Hz à 40 dB.
En produisant des sons plus aigus, une publicité peut ainsi apparaître plus sonore tout en respectant la
législation de niveau d'intensité sonore.
3.1. (0,75 pt) Le son va se propager sur la sphère de surface S = 4 π d2 = 5,03 .105 m2.
L'intensité sonore sera alors de : I' = P
S= 10 502654 = 2,0 .10 -5 W/m2
Le niveau d'intensité sonore correspondant est L' = 10 log (2,0 .10-5
1,0 .10-12) = 73 dB
3.2. (0,5 pt) Pour ce son de fréquence 500 Hz, ce niveau d'intensité sonore correspond à celui d'une
conversation. Il est raisonnable mais fatiguant à long terme et donc inacceptable si le bruit est permanent.
Ce calcul considère une propagation sans atténuation. En réalité le son est atténué par l'air. L'intensité sonore
au niveau de l'habitation est plus faible.
3.3. (0,75 pt) Le son ne sera plus perçu quand I = I0 soit lorsque S = P
I0 = 1,0 .10 13 m2 d'où d = 8,9  105 m si il
n'y a aucune atténuation du signal
3.4. (0,5 pt) Le cycliste se situe à d'' = 2d donc S'' = 4 S donc I'' = I' / 4 le cycliste entend bien un son 4 fois plus
faible.