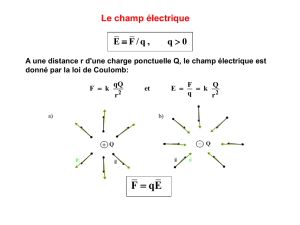
Equivalence de distances

Infty08
Equivalences de distances sur un ensemble
Soient d1 et d2 deux distances sur un ensemble X , et I : (X,d1) → (X,d2) l'application x → x ;
On adopte les définitions suivantes (attention: elles varient selon les ouvrages!):
(1) d1 ~
top d2 si I est bi-continue;
ceci équivaut à dire que (X, d1) et (X, d2) ont les mêmes ouverts, i.e. que d1 et d2 définissent la même
topologie sur X ; le cas échéant, toutes les notions topologiques concernant (X,d1) et (X,d2) (qui sont
égaux en tant qu'espaces topologiques) sont bien sûr les mêmes:
* ouverts, fermés, adhérence, intérieur, voisinages, parties denses...;
* parties compactes, parties connexes;
* continuité d'applications démarrant ou arrivant dans X;
* limites d'applications démarrant ou arrivant dans X (dont limites de suites));
...
(2) d1 ~
unif d2 si I est bi-uniformément continue; [ (2) ⇒ (1) ];
ceci équivaut à: ∀ε > 0, ∃
α
> 0, ∀x, y ∈ X: d1(x,y) ≤
α
⇒ d2(x,y) ≤ ε, et inversement; on peut
exprimer brièvement que d1 et d2 sont uniformément équivalentes si et seulement si elles "tendent
simultanément vers 0"; le cas échéant, (X,d1) et (X,d2) ont la même topologie (vu) , et la même
"structure uniforme", dans le sens: "conservation de la notion de petitesse": outre les notions
topologiques, les notions suivantes en ce qui concerne les deux espaces sont les mêmes:
* suites de Cauchy; complétude;
* continuité uniforme d'applications démarrant ou arrivant dans X;
...
(3) d1 ~ d2 si I est bilipchitzienne; [ (3) ⇒ (2) ⇒ (1)].
ceci équivaut à l'existence de deux réels
α
, β > 0 tels que
α
.d2 ≤ d1 ≤ β.d2 ; le cas échéant, outre les
notions précédemment citées, les parties bornées sont conservées (ce qui n'a pas lieu d'être pour deux
distances uniformément équivalentes).
Remarque: si X est un espace vectoriel, et d1 et d2 des distances issues de normes || . ||1 et || . ||2 sur X, alors
les trois équivalences ci-dessus coïncident.
(il suffit de vérifier (1) ⇒ (3): supposons que X1 = ( X , || . ||1 ) et X2 = ( X , || . ||2 ) ont la même
topologie; la boule B2 ( 0, 1 ) de X2 est un voisinage de 0 dans X2, et donc dans X1; elle contient par
conséquent une boule B1 ( 0,
α
) de X1 (
α
> 0); traduisant ceci, on obtient facilement:
α
.|| . ||2 ≤ || . ||1;
en inversant les rôles de X1 et X2, on conclut.
On va voir que cette propriété est très spécifique au cadre des normes sur un espace vectoriel, et ne
subsiste pas dans le cadre général des distances sur un ensemble:
Exercice: dans , on définit d par: i ) si Arg z = Arg z ' [2π], d(z,z ' ) = |z-z '| ;
ii ) sinon (y compris les cas z = 0 ou z ' = 0): d(z, z ' ) = | z | + | z ' | ;
interpréter, et montrer que d n'est pas topologiquement équivalente à la distance usuelle (regarder ses
boules ouvertes); montrer que ( ,d) est complet.
Génération de distances sur un ensemble X:
1) Soit (Y,d ) un espace métrique, et f une bijection de X dans Y:
δ
: (x,y) →
δ
(x,y) = d(f(x),f(y)) est une distance sur X (clair).
* Si X est muni d'une topologie τ , on rappelle que (X,τ) est dit métrisable si l'on peut définir sur X
une distance
δ
qui donne naissance à la topologie τ, c'est-à-dire telle que l'identité I : ( X,τ ) → (X,
δ
)
soit un homéomorphisme.
Cas d'une distance
δ
générée comme ci-dessus:
au vu du diagramme commutatif suivant, où
l'application g: t → f -1(t) est une isométrie, il est clair
que I (respt I-1) est continue si et seulement si f (respt
f -1 ) l'est. (Y,d)
fg
(X,t) (X,δ)

Infty08
Ainsi, I est un homéomorphisme si et seulement si f en est un.
Exemple: = [-∞,+∞] est muni d'un ordre total naturel qui prolonge celui de et lui confère la
topologie de l'ordre associée (les ouverts sont les réunions d'intervalles ouverts).
∀a, b ∈ , ∀fo : → ]a,b[ homéomorphisme croissant, le prolongement f : → [a,b] de f par
[ f(-∞) = a ; f(+∞) = b] est un homéomorphisme (et est compact). est donc métrisable par ce
procédé.
* Si X est déjà muni d'une distance do , et pour une distance
δ
générée comme ci-dessus:
dans le diagramme ci-contre, g: t → f -1(t) est encore
une isométrie; il s'ensuit que: I (respt I-1) est continue,
uniformément continue, lipchitzienne, si et seulement si f
(respt f -1 ) l'est;
(X,d1) (X,d2)
(Y,d)
fg
en particulier:
δ
~
top do ⇔ f : (X,do) → (Y,d) est bi-continue;
δ
~
unif do ⇔ f : (X,do) → (Y,d) est bi-uniformément continue;
δ
~ do ⇔ f : (X,d1) → (Y,d) est bi-lipchitzienne;
Exemples:
* (x,y) → |Arctg x - Arc tg y| ; (x,y) → x
1+ | x | - y
1 + | y | sur ,
(x,y) → |1/x - 1/y| sur ]0,+∞[ ,
sont topologiquement équivalentes [mais non uniformément équivalentes] à la distance
usuelle;
(x,y) → |x2-y2| sur [0,1] est uniformément équivalente [mais non équivalente] à la distance usuelle;
(x,y) → |2x-2y| sur est équivalente à la distance usuelle.
* Reprenons la métrique
δ
définie plus haut sur , et notons d la distance induite sur par
δ
, la
distance usuelle sur étant notée do : d est topologiquement équivalente à do , mais non
uniformément équivalente à celle-ci, car f -1 ne peut pas être uniformément continue (pourquoi?);
toutefois, f étant uniformément continue sur (pourquoi?), il en est de même de I: ( ,do)→(,d );
En fait, aucune distance
δ
qui métrise ne peut induire sur une distance d uniformément
équivalente à la distance usuelle do de :
preuve par l'absurde:
supposons l'identité I : ( ,do ) → ( ,d ) bi-uniformément continue;
(,
δ
) espace métrique admettant pour sous-espace dense (notion topologique);
Id : ( ,d =
δ
|) → ( ,d) est uniformément continue surjective à valeurs dans ( ,d)
complet (car d ~
unif do et ( ,do ) est complet);
le théorème de prolongement assurerait l'existence de I : ( ,
δ
) → ( ,d) continue (et
même uniformément continue) et surjective;
Or est compact et est séparé; alors serait compact, ce qui n'est pas.
2) On suppose ici X muni d'une distance d1 ; soit ϕ: [0,+∞[ → [0,+∞[ croissante, valant 0 en 0, continue en
0, strictement croissante sur un voisinage de 0, et vérifiant: [∀x,y ≥0: ϕ(x+y) ≤ ϕ(x)+ϕ(y)];
alors d2 = ϕod1 est une distance sur X, uniformément équivalente à d1;
(ϕ est localement inversible au voisinage de 0, et bi-continue en 0; il suffit de traduire cette propriété).

Infty08
Exemples: ϕ1 : t → min ( 1, t ), ϕ2 : t → t
1+t vérifient les hypothèses citées;
Remarque: la condition pour que d2 soit équivalente à d1 s'écrit: ∃
α
, β, ∀t ≥ 0, 0 <
α
≤ f(t)
t ≤ β ; cela
suppose bien entendu lim
t → +∞ ϕ(t) = +∞ ; les distances ainsi générées par les applications ϕ1 et ϕ2
précédentes ne sont donc pas équivalentes à d1 .
Réponse à un problème soulevé en leçon ( Agreg /leçon : continuité uniforme, applications) :
Au sujet de la proposition classique:
Soit ϕ : → continue, ayant des limites en +∞ et -∞ , alors ϕ est uniformément continue.
La démonstration directe utilisant le théorème de Heine sur un compact de est élémentaire;
Un étudiant a proposé le "raisonnement" suivant:
* on prolonge ϕ en une application continue
ψ
de dans ;
*
ψ
étant continue, est uniformément continue;
* par restriction, ϕ est uniformément continue.
Ceci n'a évidemment aucun sens, car il faut d'abord préciser la distance que l'on a placé sur : pour que le
raisonnement ci-dessus soit valide tel quel, il faudrait munir d'une distance
δ
qui donne naissance à sa
topologie, et dont la restriction d à soit uniformément équivalente à la distance do usuelle de : on a vu
que la première condition est réalisable ( est métrisable), mais que la seconde ne l'est pas (l'application
identique I: ( ,do ) → ( ,d) ne peut pas être uniformément continue).
En conclusion, le raisonnement précédent tel qu'il est proposé est erroné.
Faisons toutefois une remarque: soit par exemple sur la distance
δ
définie plus haut à l'aide de la fonction
f :t → Arctg t: on a vu que la continuité uniforme de f sur (car f est 1-lip) entraîne la continuité uniforme de
l'application Id : ( ,do ) → ( ,d) (et que c'est son inverse qui ne peut pas être uniformément continue); ceci
suffit pour conclure, car ϕ est la composée des applications suivantes:
(,do)
→
Id ( ,d )
→
i ( ,
δ
) →
ψ
( ,do ), toutes trois uniformément continues, donc ϕ est
uniformément continue.
(raisonnement torturé à éviter absolument!).