La réflexion totale de la lumière.

Chapitre réflexion totale. Cours SPCL - ondes Tle STL
La réflexion totale de la lumière.
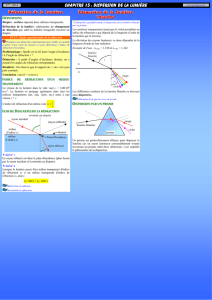
Lorsque la lumière passe vers un milieu moins réfringent (de moins grand indice
optique n ), le phénomène de réfraction fait qu'elle s'écarte de la normale au dioptre
(elle se rapproche du dioptre).
En effet, en utilisant la 2de loi de la réfraction, si on cherche l'angle réfracté i
2 :
1 1 2 2
sin( ) sin( ) n i n i
donc
1
12
2
sin(sin ) )(
ni
n
i
avec
21
nn
donc avec
1
2
1
n
n
donc
21
sin( ) sin( )
ii
donc
21
ii
.
De ce fait, si l'angle d'incidence i
1 est suffisamment grand, l'angle réfracté
i
2 devrait être supérieur à 90 ° ce qui
ne permet plus d'avoir réfraction. Donc, si l'angle d'incidence est suffisamment grand, il n'y a pas réfraction de
la lumière mais un autre phénomène : la réflexion totale de la lumière.
Rappel : l'indice optique n d'un milieu transparent est le rapport de la vitesse c de la lumière dans le vide sur la
vitesse v de la lumière dans ce milieu
/ ncv
avec c = 3,00×108 m/s
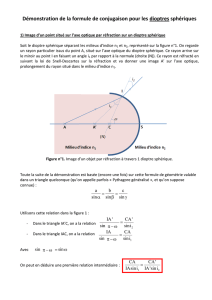
L'angle d'incidence limite (ou angle de réfraction limite) est l'angle au-delà duquel il n'y a plus réfraction mais
réflexion totale. Pour le calculer, on cherche l'angle d'incidence i
1 pour lequel l'angle réfracté
i
2 vaut 90 °.
Exemple : Sachant que l'indice optique du plexiglas vaut 1,5 , calculer l'angle de
réfraction limite d'un faisceau lumineux se propageant dans un morceau de
plexiglas placé dans l'air.
plexi plexi air air
sin( ) sin( ) n i n i
donc
air
plexi air
plexi
sin( ) sin( )
n
ii
n
donc
air
plexi air
plexi
arcsin sin( )
n
ii
n
l'angle de réfraction limite est tel que
air 90 °
i
donc
plexi limite
1,00
arcsin sin(90 ) 42 °
1,5
i
2
12
1
sin( )
n
ii
n
arcsin
s'écrit parfois sur la calculatrice
2
12
1
sin( )
n
ii
n
-1
sin
Inversement, connaissant l'angle de réfraction limite, on peut calculer l'indice optique du milieu, en prenant là
encore le cas où l'angle réfracté vaut 90 °.
Exemple : En réalisant l'étude de la réfraction avec un demi-cylindre rempli d'eau, on mesure un angle de
réfraction limite de 49 °. Déterminer l'indice de réfraction de l'eau.
eau eau air air
sin( ) sin( ) n i n i
donc
air
eau air
eau
sin( )
sin( )
i
nn i
l'angle de réfraction limite est tel que
air 90 °
i
donc
eau
sin(90 )
1,00 1,33
sin(49 )
n
Comme l'indice optique dépend (un peu) de la longueur d'onde (phénomène de dispersion de la lumière
polychromatique), l'angle de réfraction limite dépend lui aussi (un peu) de la longueur d'onde.
Les réfractomètres servent à mesurer les indices optiques des liquides. Ils utilisent le phénomène de réflexion
totale ou d'angle de réfraction limite.
Ils permettent de déterminer la concentration de certaines solutions après avoir tracé une courbe d'étalonnage.
normale (perpen-
diculaire) au dioptre
milieu 2
milieu 1
i
2
i
1
dioptre (surface
de séparation des
deux milieux)
milieu 2
milieu 1
dioptre (surface
de séparation des
deux milieux)
milieu 2
milieu 1
dioptre (surface
de séparation des
deux milieux)
milieu 2
milieu 1
dioptre (surface
de séparation des
deux milieux)
i
plexi
i
air