Polynésie-Juin

Polynésie-Juin-2014.
Exercice 2 5 points
On considère la suite
(un)
définie par :
u0
=0 et pour tout entier naturel n,
un+1=un+2n+2
1 . Calculer
u1
et
u2
.
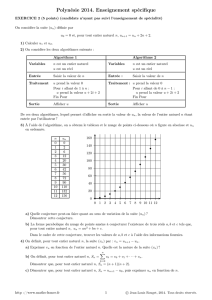
2 . On considère les deux algorithmes suivants :
De ces deux algorithmes, lequel permet d'afficher en sortie la valeur de
un
, la valeur de l'entier naturel n étant
entrée par l'utilisateur ?
3 . A l'aide de l'algorithme, on a obtenu le tableau et le nuage de points ci-dessous où figure n en abscisse et
un
en ordonnée.
a . Quelle conjecture peut-on faire quant au sens de variation de la suite
(un)
?
Démontrer cette conjecture.
b . La forme parabolique du nuage de points amène à conjecturer l'existence de trois réels a, b et c tels que,
pour tout entier naturel n,
un
=
an2
+bn+c.
Copyright  meilleurenmaths.com. Tous droits réservés Page 1
Candidats n'ayant pas suivi la spécialité

Polynésie-Juin-2014.
Dans le cadre de cette conjecture, trouver les valeurs de a, b et c à l'aide des informations fournies.
4 . On définit, pour tout entier naturel n, la suite
(vn)
par :
vn=un+1−un
a. Exprimer
vn
en fonction de n. Quelle est la nature de la suite
(vn)
?
b. On définit, pour tout entier naturel n,
Sn
=
∑
k=0
k=n
vk
=
v0
+
v1
+…
+vn
.
Démontrer que, pour tout entier naturel n,
Sn
=(n+1)(n+2)
c. Démontrer que, pour tout entier naturel n,
Sn
=
un+1
-
u0
, puis exprimer
un
en fonction de n.
Copyright  meilleurenmaths.com. Tous droits réservés Page 2

Polynésie-Juin-2014.
Correction :
1 .
u1=u0+2×0+2=0+0+2
=2
u2=u1+2×1+2=2+2+2
=6
2 . Pour l'algorithme 1,
La première valeur de i est 1
u prend la valeur
0+2×1+2
=4 or
u1
=2
Donc l'algorithme 1 ne permet pas d'afficher la valeur de
un
pour tout entier naturel n.
Pour l'algorithme 2,
La première valeur de i est 0
u prend la valeur :
0+2×0+2
=2=
u1
Donc l'algorithme 2 permet d'afficher en sortie la valeur
un
.
remarque
Il faut préciser que n est un entier naturel non nul.
3 . a. Conjecture : La suite
(un)
est croissante.
Justification :
Pour tout entier naturel n
un+1−un=2n+2
 2 > 0
donc la suite
(un)
est strictement croissante
b. Si on suppose qu'il existe des nombres réels a, b et c tels que pour tout entier naturel n :
un=an2+bn+c
Alors :
pour n=0,
u0=0=a×0+b×0+c
soit c=0
pour n=1,
u1=2=a×12+b×1+c
soit a+b+c=2
pour n=3,
u2=6=4×22+b×2+c
soit 4a+2b+c=6
On obtient :
c=0 et a+b=2 et 2a+b = 3
Donc a=1 et b=1 et c=0
S'il existe des réels a, b et c tels que pour tout entier naturel n :
un=an2+bn+c
, alors pour tout entier naturel n
on a :
un=n2+n
.
4 . On considère la suite
(vn)
définie pour tout entier naturel n par :
vn=un+1−un
a. Pour tout entier naturel n on a :
un+1−un=2n+2
donc
vn
=2n+2
(vn)
est la suite arithmétique de premier terme
v0
=2 et de raison r=2.
b. Pour tout enter naturel n
Sn
=
∑
k=0
k=n
vk
=
v0
+
v1
+ ...+
vk
+...+
vn
Sn
est la somme des n +1 premiers termes de la suite arithmétique de premier terme
v0
et de raison2
Donc,
Sn=1
2(n+1)(v0+vn)
Or,
v0
=2 et
vn
=2n+2
Copyright  meilleurenmaths.com. Tous droits réservés Page 3

Polynésie-Juin-2014.
Sn=1
2(n+1)(2+2+2n)
Sn=
( n +1)( n +2)
c.
Sn
=
v0
+
v1
+
v2
+…+
vn
Sn
=
(u1−u0)+(u2−u1)+(u3−u2)
+…+
(un+1−un)
Après simplification on obtient :
Sn=−u0+un+1
Or,
u0
=0
Donc,
Sn=un+1
On a donc,
Sn=(n+1)(n+2)=un+1
Conséquence :
Pour tout entier naturel n :
un=n(n+1)=n2+n
On a donc démontré la conjecture.
Copyright  meilleurenmaths.com. Tous droits réservés Page 4