Mouvements à force centrale

Chapitre VII
M `  
VII.. Lois de Kepler
En première approximation, le mouvement des planètes (∗1) autour du Soleil est régi par trois lois qui
furent établies au 17esiècle par l’astronome Johannes Kepler, à partir notamment des observations de
Mars réalisées par Tycho Brahe. Ces lois furent utilisées par Newton pour établir la loi de l’attraction
universelle. Voici leur énoncé traditionnel :
Première loi de Kepler
Les planètes décrivent des ellipses dont le Soleil est l’un des foyers.
Deuxième loi de Kepler
Le rayon-vecteur (c.-à-d.le segment) Soleil-planète balaie des aires égales en des temps égaux.
Troisième loi de Kepler
Le rapport du cube du demi-grand axe de l’ellipse sur le carré de la période de révolution autour
du Soleil est le même pour toutes les planètes.
Nous démontrerons ces lois et préciserons leur signification et leurs limites dans ce qui suit.
VII.. Mobile fictif
Soient R=(O,~ ı, ~ , ~ k) un référentiel galiléen et M1et M2deux points matériels de masses m1et m2.
Notons Gle centre d’inertie du système S={M1,M2}:
m1−−−→ GM1+m2−−−→ GM2=~ 0.
On suppose que Sest un système isolé. On a donc (m1+m2)~ aG/R=P~ Fext→S=~ 0, c.-à-d.~ vG/R=~ cte :
le référentiel barycentrique R∗=(G,~ ı, ~ , ~ k) de Sest donc galiléen.
On se place désormais dans R∗.
Z
On définit le mobile fictif Mpar −−−→
GM B−−−−−→ M1M2B~ r
1. Rappelons que, par ordre croissant de distance au Soleil, les planètes du Système solaire sont Mercure, Vénus, la Terre,
Mars, Jupiter, Saturne, Uranus et Neptune. Elles effectuent leurs révolutions autour du Soleil quasiment dans le même
plan que la Terre. Ce dernier, appelé écliptique, est incliné d’environ 23◦par rapport à l’équateur terrestre.
75

Michel F Dynamique des systèmes
et on lui associe la masse réduite
µBm1m2
m1+m2.
Connaissant la position du mobile fictif, il est facile d’en déduire celles de M1et M2. En effet,
−−−→
GM1=−−−→ GM2+−−−−→ M2M1=−m1−−−→ GM1/m2−~ r, donc
−−−→
GM1=−m2
m1+m2~
r.
De même, −−−→
GM2=m1
m1+m2~
r.
En particulier, si m2m1(p.ex.la masse d’un satellite devant celle de la Terre ou la masse d’une
planète devant celle du Soleil), −−−→ GM1≈~ 0 et −−−→ GM2≈~ r:M1est alors presque confondu avec G, et M2avec
M.
Z
La trajectoire de Mest déterminée par
~
F1→2=m2d2−−−→
GM2
dt2=µd2~
r
dt2.
On a
~
LG({M1,M2})=m1−−−→ GM1×d−−−→
GM1
dt+m2−−−→
GM2×d−−−→
GM2
dt
=m1−−−→ GM1×d−−−→
GM1
dt+m2−−−→
GM2×d(−−−→
GM1+−−−−→ M1M2)
dt
=(m1−−−→ GM1+m2−−−→ GM2
| {z }
~
0
)×d−−−→
GM1
dt+m2−−−→
GM2
| {z }
µ~ r
×d−−−−→
M1M2
dt,
soit
~
LG({M1,M2})=µ~ r×d~
r
dtB~
LG(M).
De même,
Ec({M1,M2})=1
2µ·d~
r
dt2
BEc(M).
VII.. Constantes du mouvement
VII..1. Moment cinétique. 2eloi de Kepler
Le système étant isolé, ~ LG=~ cte. Notons ~ uzun vecteur unitaire colinéaire à ~ LGet L0=~ LG·~ uz.
Le vecteur ~ rétant perpendiculaire à ~ LG, donc à un vecteur ~ uzconstant, M se déplace dans le plan
perpendiculaire à ~ LGpassant par G. Soient ~ uxet ~ uydeux vecteurs tels que le repère (G,~ ux,~ uy,~ uz) soit
orthonormé direct. Repérons Mpar ses coordonnées polaires, r=k−−→ GMket φ=(~ uxb,−−→ GM). On a
~
LG(M)=µ~ r×d~
r
dt=µ·(r~
ur)×(. r~ ur+r. φ~ uφ)=µr2. φ~ uz.
La constante
CBr2. φ=L0/µ
s’appelle la constante des aires (∗2).
2. Certains auteurs appellent « constante des aires» la quantité C/2.
76

Chapitre VII. Mouvements à force centrale
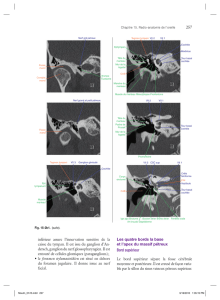
Pendant une durée infinitésimale dt, l’aire balayée par le rayon-vecteur −−→ GM vaut (cf.§ I..1 pour
le calcul de l’aire d’un triangle)
dA=k~
r×d~ rk
2=|C| 2dt.
C’est ce qu’exprime la loi des aires, ou 2eloi de Kepler : « Le rayon-vecteur balaie des aires égales en
des temps égaux. ».
L’aire A1balayée par −−→ GM entre
t1et t1+ ∆test égale à l’aire A2
balayée entre t2et t2+ ∆t.
Cas où m1m2
Si m1m2,~ LM1(M2)=~ LG(M), donc ~ LM1(M2)=~ cte.
On peut démontrer ceci sans passer par le mobile fictif. Si m1m2,M1est confondu avec Get est
donc immobile dans R∗. En appliquant le théorème du moment cinétique à M2seul et en calculant
les moments par rapport à M1, on obtient d~ LM1(M2)/dt=−−−−→ M1M2×~ F1→2=~ 0, puisque ~ F1→2est une force
centrale.
VII..2. Énergie mécanique. Énergie potentielle effective
M1et M2interagissent par l’intermédaire d’une force centrale, c.-à-d.une force dirigée selon −−−−→ M1M2
et ne dépendant que de r=k−−−−→ M1M2k. Une telle force est nécessairement conservative. Le système étant
isolé, son énergie mécanique, Em=Ec+Ep, est donc constante ; notons-la E0. On a
E0=1
2µ·(.
r2+r2. φ2)+Ep(r)=1
2µ· .
r2+r2·C
r22!+Ep(r)=1 2µ.
r2+Eeff
p(r),
où
Eeff
p(r)BµC2
2r2+Ep(r)
est l’énergie potentielle effective.
Z
On peut séparer les variables tet rdans l’équation différentielle (en ret . r) ci-dessus. On obtient
dt=dr
q2 (E0−Eeff
p[r])/µ ,
que l’on peut intégrer pour trouver ten fonction de r.
On a de même
dφ=Cdr
r2q2 (E0−Eeff
p[r])/µ .
77

Michel F Dynamique des systèmes
Cas d’une force en 1/r2
Considérons le cas d’une force en 1/r2,
~
F1→2=−K
r2~
ur.
K=Gm1m2correspond à la force gravitationnelle et K=−q1q2/(4 π 0) à la force électrostatique. ~ F1→2
dérive alors de l’énergie potentielle d’interaction
Ep=−K
r
et
Eeff
p=µC2
2r2−K r.
On a . r2=2 (E0−Eeff
p)/µ. Les seules valeurs de rpossibles sont donc celles pour lesquelles Eeff p(r)6E0.
Distinguons les cas suivants :
1. K>0.
On a limr→0Eeff
p= +∞et limr→∞ Eeff p=0−. La fonction Eeff pa un minimum négatif unique en
r0=µC2 /K.
a.E0>0.
L’équation E0−Eeff
p(r)=0 n’a qu’une seule racine, rmin. On a alors r>rmin : la trajectoire
s’étend jusqu’à l’infini.
b.E0<0.
L’équation E0−Eeff
p(r)=0 a deux racines, rmin et rmax (rmax >rmin). On a alors rmin 6
r6rmax : la distance entre M1et M2est bornée.
2. K<0.
On a limr→0Eeff
p= +∞et limr→∞ Eeff p=0+. La fonction Eeff pest strictement décroissante.
Comme dans le cas 1.a,E0>0 et l’équation E0−Eeff
p(r)=0 n’a qu’une seule racine, rmin. On a
alors r>rmin : la trajectoire s’étend jusqu’à l’infini.
78

Chapitre VII. Mouvements à force centrale
Les points Pet Acorrespondant à r=rmin et r=rmax s’appellent respectivement le péricentre et
l’apocentre. Dans le cas particulier d’un corps tournant autour de la Terre, on parle plutôt de périgée
et d’apogée ; autour du Soleil, de périhélie et d’aphélie ; autour d’une autre étoile, enfin, de périastre
et d’apoastre.
VII.. Coniques
VII..1. Généralités
Considérons un cercle Cet un point Ssitué hors du plan de C, sur la droite passant par le centre
de Cperpendiculaire au plan de C. L’ensemble des droites passant par Set s’appuyant sur Cforme
un cône, K, de sommet S.
Les coniques sont les courbes correspondant à l’intersection d’un plan Pavec K:
•Si Pest peu incliné par rapport au plan de C, on obtient une courbe fermée, l’ellipse.
Le cercle est un cas particulier d’ellipse obtenu si Pest parallèle à C.
•Inclinons un peu plus P. À un certain moment, Pdevient parallèle à l’une des droites génératrices
du cône ; on a alors une courbe ouverte, la parabole.
•Si nous inclinons encore plus P, le plan coupe le cône de part et d’autre de son sommet. On
obtient une courbe ouverte constituée de deux branches, l’hyperbole.
À la limite, si le plan passe par S, on obtient deux droites.
VII..2. Foyer, excentricité
On peut également définir les co-
niques de la manière suivante : considé-
rons une droite ∆(la « directrice »), un
point Fet un nombre e>0.
La conique de foyer Fet
d’excentricité eest l’ensemble des
points Mtels que
k−−→ FMk
k−−→ HMk
=e,
où Hest la projection orthogonale de M
sur ∆.
Si e<1, la conique est une ellipse
(en particulier un cercle si e=0) ; si
e=1, c’est une parabole ; si e>1, une
hyperbole.
Si la conique est une ellipse ou une hyperbole, il existe un deuxième foyer, F0, et une deuxième
directrice, ∆0, donnant la même courbe.
VII..3. Équation en coordonnées polaires
Notons Kla projection orthogonale de Fsur ∆,h=k−→ FKk,~ ux=−→ FK/h(donc k~ uxk=1) et ~ uyun vecteur
unitaire parallèle à ∆.
Dans le repère orthonormé (F,~ ux,~ uy), l’équation en coordonnées polaires de la conique est
r=p
1+ecos φ,
où rBk−−→ FMk,φB(~ uxb,−−→ FM) et pBe h.
Dans le cas de l’hyperbole, il s’agit de l’équation de la branche située en deçà de la directrice par
rapport à F. L’équation de la branche située au-delà est
r=p
ecos φ−1.
79