Un cours

5ème 4 2009-2010
Chapitre n°4 : « Angles, caractérisation du
Chapitre n°4 : « Angles, caractérisation du
parallélisme »
parallélisme »
I.
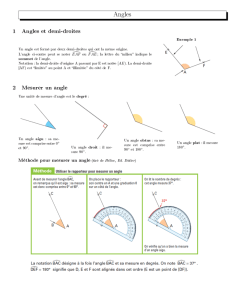
I. Reproduire un angle ; rappels Reproduire un angle ; rappels
1/
1/ Mesurer un angle Mesurer un angle
(Voir fiche d'exercices)
2/
2/ Construire un angle de mesure donnée Construire un angle de mesure donnée
Construire les angles suivants :
ACB=57°
et
EFJ =123°
Méthode
Méthode
•On trace une demi-droite ; son origine est le sommet de l'angle.
•On place le centre du rapporteur sur l'origine de la demi-droite et le zéro d'une
graduation au niveau de cette même demi-droite.
•On trace une deuxième demi-droite passant par la graduation correspondant à la
mesure de l'angle.
3/
3/ Reproduire un angle Reproduire un angle

5ème 4 2009-2010
II.
II. Propriétés sur les paires d'angles Propriétés sur les paires d'angles
1/
1/ Angles opposés par le sommet Angles opposés par le sommet
Activité
Activité
Les angles suivants ne sont pas opposés par le sommet.
L'angle suivant est opposé par le sommet.
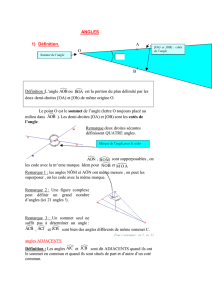
Définitions
Définitions
Deux angles opposés par le sommet sont deux angles qui ont le même sommet et sont
symétriques par rapport à ce sommet.
Représentation
Représentation
Il suffit de tracer deux droites sécantes. Elles définissent deux paires d'angles opposés
par le sommet.
Propriété
Propriété
Des angles opposés par le sommet sont de la même mesure.

5ème 4 2009-2010
2/
2/ Angles adjacents Angles adjacents
Activité
Activité
•Ces deux angles ne sont pas adjacents car ils n'ont pas le
même sommet.
•Ces deux angles sont adjacents : ils ont le même sommet et
un côté en commun.
•Ces deux angles ne sont pas adjacents car l'un
contient l'autre.
Définition
Définition
Deux angles sont adjacents si :
•ils ont le même sommet ;
•ils ont un côté en commun ;
•ils sont situés de part et d'autre du côté en
commun.
Exemple
Exemple
LOM
et
MON
sont adjacents car :
•
O
est le sommet commun ;
•
[OM 
est le côté commun ;
•les deux angles sont « distincts » (pas l'un dans l'autre).
3/
3/ Angles complémentaires Angles complémentaires
Définition
Définition
Deux angles sont complémentaires si la somme
de leurs mesures est égale à
90°
.
Exemple
Exemple
Les angles ci-contre
IEJ
et
KHL
sont
complémentaires car
3456=90 °
.

5ème 4 2009-2010
Autres exemples
Autres exemples
•
ABD=36 °
et
EFR=54°
sont complémentaires car
3654=90
.
•
FRT =46°
et
GHJ =45°
ne sont pas complémentaires car
4645≠90
.
•Les angles
A ' BA
et
C ' DC
sont complémentaires car la
somme de leurs mesures est
4149=90
.
Cas particulier : angles adjacents formant un angle droit
Cas particulier : angles adjacents formant un angle droit
Propriété
Propriété
Deux angles adjacents qui forment un angle droit sont complémentaires.
Exemple
Exemple
Dans la figure ci-contre :
EOF
et
GOF
sont adjacents car
O
est le sommet en commun,
[OF 
est le côté en
commun et ils sont de part et d'autre de ce côté
[OF 
;
l'ensemble des deux angles
EOF
et
GOF
forment l'angle
droit
EOG
.
On a donc
EOF  GOF =90°
.
Application
Application
Dans la figure ci-contre, on peut calculer
BIC
:
BIC=90 –55=45 °
car
BIC
et
BIA
sont
complémentaires.
Les angles
AIB
et
BIC
sont adjacents car :
•
I
est le sommet commun ;
•
[IB 
est le côté commun ;
•les angles sont de part et autre de
[IB 
.
AIB
et
BIC
forment l'angle droit
AIC
; ils sont donc complémentaires .
On a donc :
BIC =90 –55=25°
.

5ème 4 2009-2010
4/
4/ Angles supplémentaires Angles supplémentaires
Définition
Définition
Deux angles sont supplémentaires si la somme de leurs mesures est égale à
180°
.
Exemple
Exemple
ABC
et
DEF
sont supplémentaires car
10278=180°
Propriété
Propriété
Deux angles adjacents formant un angle plat sont
supplémentaires.
Exemple
Exemple
Si
BCD
et
DCA
sont adjacents et forment un angle plat et si
BCD=53 °
alors
DCA=180 –53=127 °
.
5/
5/ Angles alternes-internes Angles alternes-internes
Activité
Activité
A l'oral....