Devoir Maison Correction

Devoir Maison Correction
TS
1
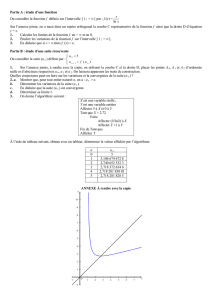
1. On considère l’algorithme suivant :
Entrée Saisir un réel strictement positif non nul a
Saisir un réel strictement positif non nul b (b > a)
Saisir un entier naturel non nul N
Initialisation Affecter à u la valeur a
Affecter à v la valeur b
Affecter à n la valeur 0
Traitement TANTQUE n < N
Affecter à n la valeur n +1
Affecter à u la valeur 
Traitement Affecter à v la valeur 
Affecter à a la valeur u
Affecter à b la valeur v
Sortie Afficher u, afficher v
Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour a = 4, b = 9 et N = 2. Les
valeurs successives de u et v seront arrondies au millième.
n
a
b
u
v
0
4
9
4
9
1
6,5
6,964
6,5
6,964
2
6,732
6,736
6,732
6,736
Dans la suite, a et b sont deux réels tels que 0 < a < b.
On considère les suites (un) et (vn) définies par :
u0 = a, v0 = b et, pour tout entier naturel n :
2. a. Démontrer par récurrence que, pour tout entier naturel n, on a : un > 0 et vn > 0.
Posons Hn l’hypothèse de récurrence 
Initialisation :
u0 = a > 0 et v0 = b > a > 0.
Donc H0 est vraie.
Hérédité :
Supposons qu’il existe un rang n pour lequel Hn soit vraie, c’est-à-dire :
Montrons que Hn+1 est vraie, c’est-à-dire :   
Or d’après Hn, on a :  
De plus vn+1 est la racine carrée de nombres positifs donc vn+1 > 0.
On peut donc dire que Hn+1 est vraie.
Conclusion : Pour tout entier naturel n, on a Hn vraie.

Devoir Maison Correction
TS
2
b. Démontrer que, pour tout entier naturel n :
En déduire que, pour tout entier naturel n, on a un vn.
D’après ce qui précède, on a :
La fonction racine carrée étant croissante sur [0 ;+[, on peut donc conclure que un vn.
3. a. Démontrer que la suite (un) est croissante.
On peut donc conclure que la suite U est croissante.
b. Comparer vn+1² et vn². En déduire le sens de variation de la suite (vn).
De plus un  vn  un² vn². On peut donc conclure que vn+1² n²  vn+1 n. La suite V est donc décroissante.
4. Démontrer que les suites (un) et (vn) sont convergentes.
La suite U est croissante et majorée par v0 donc elle converge.
La suite V est décroissante et minorée par u0 donc elle converge.