NOM Prénom : TEST mercredi 16 novembre 2016 BTS N°1 : Soit f(x

NOM Prénom :
TEST mercredi 16 novembre 2016 BTS
N°1 : Soit f(x) = 6 . Calculer la fonction dérivée de f.
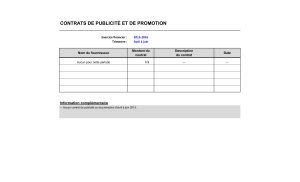
N°2 : Un grossiste achète des boites de thé vert chez deux fournisseurs.
Il achète 80 % de ses boîtes chez le fournisseur A et 20% chez le fournisseur B.
10% des boites provenant du fournisseur A présentent des traces de pesticides
Et 20 % de celles provenant du fournisseur B présentent aussi des traces de
pesticides.
On prélève au hasard une boîte du stock du grossiste et on considère les évènements
suivants : A : « la boîte provient du fournisseur A »
S : « la boîte présente de traces de pesticides »
Dans cet exercice, tous les résultats seront arrondis au centième.
a. Traduire l’énoncé sous la forme d’un arbre pondéré.
b. Décrire par une phrase, les probabilités ; pA(S) ; p(AS) ; p( 
 ) .
Déterminer une valeur des probabilités citées précédemment.
c. Déterminer la probabilité que la boîte prélevée présente des traces de pesticide.
d. Démontrer que la probabilité qu’une boîte ne présente pas de traces de pesticides
est de 0,88.
e. Déterminer la probabilité qu’une boîte provienne du fournisseur B sachant qu’elle
présente des traces de pesticides. (On commencera par traduire cette probabilité en
utilisant les notations vues en classe.)
Barème : n°1 : 1 point n°2 : a. 1 b. 1,5 c. 1 d. 0,5 e. 1 total : 5 points
TOTAL : 6 points :
NOM Prénom :
TEST mercredi 16 novembre 2016 BTS
N°1 : Soit f(x) = 6 . Calculer la fonction dérivée de f.
N°2 : Un grossiste achète des boites de thé vert chez deux fournisseurs.
Il achète 80 % de ses boîtes chez le fournisseur A et 20% chez le fournisseur B.
10% des boites provenant du fournisseur A présentent des traces de pesticides
Et 20 % de celles provenant du fournisseur B présentent aussi des traces de
pesticides.
On prélève au hasard une boîte du stock du grossiste et on considère les évènements
suivants : A : « la boîte provient du fournisseur A »
S : « la boîte présente de traces de pesticides »
Dans cet exercice, tous les résultats seront arrondis au centième.
a. Traduire l’énoncé sous la forme d’un arbre pondéré.
b. Décrire par une phrase, les probabilités ; pA(S) ; p(AS) ; p( 
 ) .
Déterminer une valeur des probabilités citées précédemment.
c. Déterminer la probabilité que la boîte prélevée présente des traces de pesticide.
d. Démontrer que la probabilité qu’une boîte ne présente pas de traces de pesticides
est de 0,88.
e. Déterminer la probabilité qu’une boîte provienne du fournisseur B sachant qu’elle
présente des traces de pesticides. (On commencera par traduire cette probabilité en
utilisant les notations vues en classe.)
Barème : n°1 : 1 point n°2 : a. 1 b. 1,5 c. 1 d. 0,5 e. 1 total : 5 points
TOTAL : 6 points :

CORRECTION TEST mercredi 16 novembre 2016 BTS
N°1 : Soit f(x) = 6 .       
N°2 : Un grossiste achète des boites de thé vert chez deux fournisseurs.
Il achète 80 % de ses boîtes chez le fournisseur A et 20% chez le fournisseur B.
10% des boites provenant du fournisseur A présentent des traces de pesticides
Et 20 % de celles provenant du fournisseur B présentent aussi des traces de
pesticides.
a.
b. pA(S) = 0,1 : probabilité qu’il y ait des traces de pesticides
sachant que la boîte provient du fournisseur A.
p(AS) = 0,80,1 = 0,08 : probabilité qu’il y ait des traces de pesticides
et que la boîte provienne du fournisseur A.
p( 
 ) = 0,2 : probabilité que la boîte provienne du fournisseur B.
c. Probabilité que la boîte prélevée présente des traces de pesticide. :
p(S) = p(A  S ) + p( B  S) = 0,8 0,1 + 0,2  0,2 = 0,08 + 0,04 = 0,12
d. Probabilité qu’une boîte ne présente pas de traces de pesticides :
p( 
 ) = 1 – p(S) = 1 – 0,12 = 0,88.
e. Probabilité qu’une boîte provienne du fournisseur B sachant qu’elle présente des
traces de pesticides : pS(B) = 
 =   0,333
Barème : n°1 : 1 point n°2 : a. 1 b. 1,5 c. 1 d. 0,5 e. 1 total : 5 points
TOTAL : 6 points :