Angles ( PDF

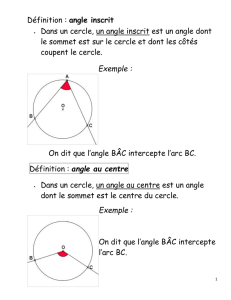
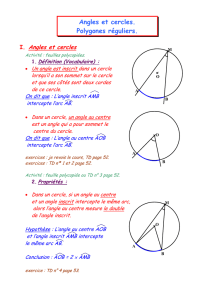
ANGLES INCRITS – ANGLES AU CENTRE
Exercice 1 :
Le point A est le centre du cercle passant par les points B, C, F, E et D.
a) Citer des angles inscrits qui interceptent l'arc BD.
b) Citer l'angle au centre qui interceptent l'arc CF.
c) Citer l'angle au centre et un angle inscrit qui interceptent le même arc EF.
Exercice 2 :
Les points A, B, E et D sont sur le cercle (C) de centre O.
a) Citer deux angles au centre du cercle (C) en précisant l'arc de cercle qu'ils
interceptent.
b) Citer deux angles inscrits dans le cercle (C) qui interceptent l'arc AB.
c) Citer dans le cercle (C) un angle inscrit et l'angle au centre qui
interceptent l'arc BE.
Exercice 3 :
a) Le point O est le centre du cercle tracé (figures de gauche). Préciser si les deux angles
colorés interceptent le même arc de cercle.
b) Le point E est le centre du cercle tracé (figures de droite). Déterminer la mesure de l'angle
colorié.
Exercice 4 :
a) Reproduire la figure.
b) Repasser en rouge le petit arc AB.
c) Marquer en vert l'angle au centre qui intercepte le petit arc AB.
d) Marquer et nommer un angle inscrit qui intercepte le petit arc
AB. Que peut-on dire de sa mesure ?
e) Reproduire une nouvelle fois la figure.
f) Repasser en rouge le grand arc KB.
g) Marquer en vert l'angle au centre qui intercepte le grand arc KB.
h) Sachant que KAB = 152°, quelle est la mesure de l'angle vert ?
i) Justifier que KTB = 28°

Exercice 5 :
Sur la figure ci-contre, les points F, G, H et K sont sur le cercle (C) de
centre O. Les droites (FH) et (GK) sont sécantes au point T.
a) Déterminer la mesure de l'angle GKF, puis celle de KFH.
b) En déduire la mesure de l'angle KTF.
Exercice 6 :
Sur la figure, A, B et C sont des points du cercle (C) de centre O tels que
AOB = 72° et BOC = 52°. Calculer la mesure de chacun des angles du
triangle ABC.
Exercice 7 :
Sur la figure, E, D, F, S et T sont des points du cercle (C) de centre J. Un
élève annonce : « J'ai rangé ces trois angles par ordre croissant de
mesures : TFS, TES et TDS. » Qu'en pensez-vous ?
Exercice 8 :
Lors d'une séance d'entraînement aux tirs au but en hockey sur glace,
quatre joueurs sont placés sur un arc de cercle comme l'indique la figure.
Le but est représenté par le segment [BU]. Lequel de ces quatre joueurs a
le plus grand angle de tir ?
Exercice 9 :
a) Construire un cercle de centre O de rayon 4 cm et placer deux points A et B tels que AOB =
90°. Placer deux points M et N sur ce cercle, de sorte que M appartienne au quart de cercle
d'extrémités A et B et que N n'appartienne pas à ce quart de cercle.
b) Donner la mesure de l'angle ANB puis celle de AMB.
c) Une élève affirme : « Les angles AMB et ANB sont complémentaires. » Est-ce exact ?
Exercice 10 :
a) Construire un triangle RST tel que RS = 7cm, SRT = 30° et RST = 40°.
b) Construire le cercle circonscrit au triangle RST. Noter O son centre.
c) Déterminer la mesure des angles TOR, TOS et ROS.

Exercice 11 :
a) O est le centre du cercle. Dans chaque cas, dire si l'angle marqué est un angle inscrit.
b) O est le centre du cercle. Dans chaque cas, dire si l'angle marqué est un angle au centre.
c) O est le centre du cercle. Dans chaque cas, dire si l'angle inscrit et l'angle au centre
interceptent le même arc.
d) O est le centre du cercle. Dans chaque cas, donner la mesure de l'angle AMB. Citer la
propriété utilisée.
e) A, M et B sont trois points d'un cercle de centre O tels que AMB = 36°. Une élève affirme :
« L'angle AOB mesure 70°. Je l'ai mesuré avec mon rapporteur. » Sa voisine lui rétorque :
« Alors là, je peux te dire que tu te trompes ! » Qu'en pensez-vous ?
f) A, B et C sont trois points d'un cercle de centre O tels que BAC = 50°. Donner
la mesure des angles BOC, OBC et OCB.
g) Les points A, B, C et D appartiennent à un cercle. ADC = 65° et
BAD = 40°. Les cordes [AB] et [CD] se coupent en I. Donner la
mesure des angles ABC, BCD et BIC.
Défi 12 :
Un footballeur recherche sur un terrain de football les positions desquelles il pourra tirer dans
le but sous un angle de 20°. Comment déterminer ces différentes positions ?