Télécharger

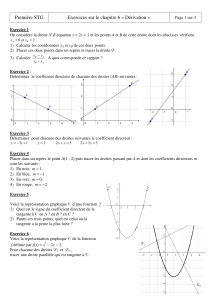
Exercice 5
Déterminez les tangentes ( quelles équations
réduites et en quels points ) à la courbe de la
fonction f définie sur R par f(x) = x² + 3x + 1
passant par le point B( - 3 ; - 3 ). Faites d’abord
une recherche graphique, avant une
détermination algébrique.

Recherche graphique :
f est une fonction polynôme de degré 2, donc sa
courbe est une parabole.

Recherche graphique :
f est une fonction polynôme de degré 2, donc sa
courbe est une parabole.
a = 1 > 0 donc la parabole est orientée vers le
haut.

Recherche graphique :
f est une fonction polynôme de degré 2, donc sa
courbe est une parabole.
a = 1 > 0 donc la parabole est orientée vers le
haut.
Elle est symétrique par rapport à la droite
d’équation x = - b/(2a) = - 3/(2(1)) = - 3/2

Recherche graphique :
f est une fonction polynôme de degré 2, donc sa
courbe est une parabole.
a = 1 > 0 donc la parabole est orientée vers le
haut.
Elle est symétrique par rapport à la droite
d’équation x = - b/(2a) = - 3/(2(1)) = - 3/2
Je peux déterminer son sommet S( - 3/2 ; f(- 3/2 )) = ( - 3/2 ; - 5/4 )