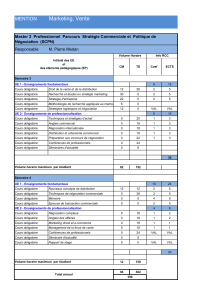
p et q

Vers une interprétation
« concrète »
•Le système formel, que nous appellerons
calcul booléen, a reçu une interprétation
mathématique rigoureuse au moyen du
domaine D = {0, 1} et des opérations + et
définies sur lui,
•Maintenant, « concrètement » quelle
signification donner à des variables qui ne
peuvent prendre pour valeurs que 0 ou 1?

Calcul propositionnel
• Une candidate à la signification qu’on peut
accorder à une variable booléenne est la
notion logique de proposition,
•Une proposition est une entité qui est soit
vraie (1) soit fausse (0)
•Le calcul propositionnel est donc une
« interprétation concrète » du calcul
booléen quand 1 est interprété comme
Vrai (v) et 0 comme Faux (f)

Remarque
• On ne parle pas ici d’ « interprétation » au sens
rigoureux du terme, c’est-à-dire au sens où on
pourrait calculer ce qui est vrai dans
l’interprétation pour connaître par avance ce
qu’on peut démontrer comme théorème dans le
système,
•En effet les seules « vérités » de la logique nous
sont accessibles par l’intuition… qui n’est pas
un calcul à proprement parler, ou alors il faudrait
tabler sur une méthode de calcul… que nous ne
possédons pas encore (puisque nous sommes
en train de l’élaborer!)

suite
•Le calcul propositionnel est donc une
algèbre de Boole où les variables,
appelées variables propositionnelles,
représentent des propositions, c’est-à-
dire des entités ayant pour valeurs
possibles: le vrai (v) ou le faux (f)
•Les opérations booléennes déjà
introduites s’interprètent aisément

connecteurs
•Dans le cas du calcul propositionnel (dorénavant CP),
les opérations booléennes sont interprétées comme des
connecteurs,
•Un connecteur binaire est une manière de composer
deux propositions pour en obtenir une troisième,
• Un connecteur unaire est une manière d’obtenir une
autre proposition à partir d’une proposition donnée
• On peut ainsi définir « récursivement » ce qu’on entend
par une proposition (au sens général):
–Une variable propositionnelle est une proposition,
–Si P et Q sont des propositions et si © est un connecteur binaire,
alors P © Q est une proposition
–Si P est une proposition et si ® est un connecteur unaire, alors
®P est une proposition