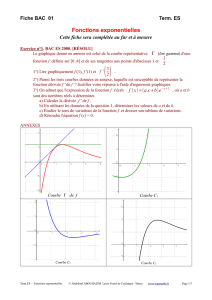
P n - Alain Lecomte

Logique et raisonnement
scientifique
cours transversal
Collège Doctoral
Pr. Alain Lecomte

7- La logique intuitionniste
de Heyting et Kripke à
la correspondance de
Curry-Howard

Système déductif (déduction naturelle)
: de , A |-- B
on peut déduire :
|-- A B
A, B |-- A B
A |-- A B
B |-- A B
A, A B |-- B
(modus ponens)
A B |-- A
A B |-- B
de , A |-- C et
, B |-- C
on peut déduire :
, A B |-- C

arbres
Élimination de Introduction de 
AA B
B
[A]x
B
A Bx

arbres
Élimination de Introduction de 
A B
A B
A BA B
A B