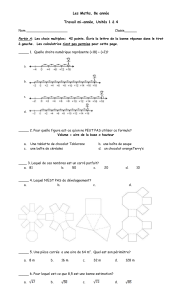
rappel sec 3 : probabilité géométrique

Probabilités géométriques

Probabilité géométrique
La probabilité géométrique est liée à la réalisation d’un résultat d’une
expérience aléatoire dans un contexte géométrique.
La formule : P = Aire favorable
Aire de la surface totale
Regardons quelques exemples:

Exemple 1: Dans la figure suivante, quelle est la
probabilité d’atteindre le cercle ?
La formule : P = Aire du cercle
Aire de la surface totale
1) Calculer l’aire du cercle:
A = πr2= πX 22≈ 12,5664 cm2
2) Calculer l’aire du carré:
8 cm
2 cm
8 cm
A = C2= 82= 64 cm2
3) Poser le rapport: P = Aire du cercle
Aire de la surface totale
=64 cm2
12,5664 cm2
≈ 0,196
La probabilité d’atteindre le cercle est donc d’environ 19,6 %.
≈ 19,6 %

Exemple 2:
12 cm
6 cm
Quelle est la probabilité d’atteindre un des
carrés rouges ?
1) Calculer l’aire d’un carré:
A = C2= 32= 9 cm2
2) Calculer l’aire du rectangle:
A = L X l = 12 X 6 = 72 cm2
3) Poser le rapport: P = Aire des cibles
Aire de la surface totale
=9 cm2+ 9 cm2
72 cm2
=
18 cm2
72 cm2=
4
1= 0,25 = 25 %
La probabilité d’atteindre un des carrés rouges est de 25 %.
La probabilité d’atteindre un des carrés jaunes est alors de :
P( carré jaune ) = 1 –P( carré rouge ) = 1 –25 % = 75 %