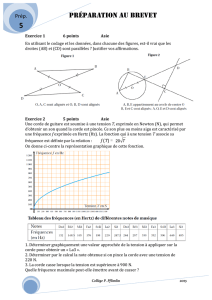
powerpoint 2003 - Site de jacques bretin

QUELQUES
ALGORITHMES
DANS 5 500
ANS
D’HISTOIRE

Quelques dates importantes au proche orient (en gros): En très gros
-100 000 : Apparition de l’homo sapiens-sapiens. NOUS
-11 000 : Premiers sédentaires, premières « maisons » au proche orient.
-10 000 : Début de l’agriculture: Apparition du …. TRAVAIL
-9 000 : Début de l’élevage.
- 5 000 : Premiers villages conséquents; il ya suffisamment à manger pour tous, la
population s’accroît, hiérarchisation de la société: Naissance de l’aristocratie qui ne
travaille pas… donc apparition de … L’IMPOT
- 3 500 : Premières villes, cités états: Nombreux corps sociaux différents (clergé au
service de l’aristocratie divine, artisans, fonctionnaires …). Pour payer tous ces gens,
les rois doivent avoir un système d’imposition efficace: il faut savoir calculer,
n’oublier personne. Deux outils deviennent vite indispensable : L’ECRITURE, LE CALCUL
Ainsi les mathématiques procèdent de l’impôt…
A partir de -2 500 : Résolution d’équations (premier et second degré), relation de
Pythagore etc.
Points de repère: Hammourabi : -1800 Ramsès II: -1300
Assurbanipal :-669 Thalès -625/-547 Nabuchodonosor : -600
Pythagore -580/-497 Aristote -384/-322 Alexandre: -350
Euclide -325/-265 Archimède -287/-212 Diophante 200/284

MESOPOTAMIE

1 chevron = 10
3 chevrons =30
1 clou = 1
2 clous =2
1 ; 24 , 51 , 10 = 1 + 24/60 + 51/602+ 10/ 603≈ 1, 41421296
30 ×1, 41421296 ≈ 42, 4263870 = 42; 25 , 34 , 59 …
L’algorithme « de
Babylone» permet
de calculer les
racines carrées de
manière très
efficace…
Diapo largement inspiré des travaux de Gilles Aldon et Michel Mizony:
http://rallye-math.univ-lyon1.fr/2007/Conference/conf2.pdf
Une tablette de -2500

L’algorithme de Babylone: calcul d’une racine carrée
On part d’un rectangle (21), on cherche la moyenne des longueurs des côtés:
(2+1)/2 = 3/2 = 1;30 qui sera notre nouvelle longueur.
On cherche la nouvelle largeur de sorte que l’aire du nouveau rectangle soit toujours 2.
2/1;30 = 1;20. On obtient notre nouveau rectangle (1;30 1;20).
On réitère: (1;25 1;24,42,10).
Et encore: (1;24,51,10,35 1;24,51,9,40): c’est la valeur de la tablette: 1;24,51,10.
L’algorithme pour calculer la
racine de A est donc:
(x,y)( (x+y)/2 , 2A/(x+y) )
en initialisant à (1,A)