Cerf-volant : commentaires sur une activité en classe

Un exemple d'activité avec Géoplan
A proposer aux élèves à partir d'une figure donnée :
•Construire cette figure avec Géoplan
•Identifier les quadrilatères obtenus
•Initier le raisonnement à partir de propriétés
•Construire la figure avec les instruments
•Rédiger un programme de construction
"De la médiatrice au cerf-volant et au losange"

A partir de l'analyse de la figure du fichier « Cerf-volant MCL.g2w » :
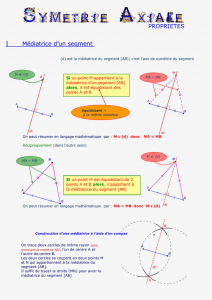
Utilisation de la propriété caractéristique de la médiatrice d'un segment
pour montrer que AB = BC et AD = DC
On peut ainsi définir un cerf-volant comme un quadrilatère qui possède deux
paires de côtés consécutifs de même longueur.
Mise en évidence de la médiatrice de [AC] comme axe de symétrie.
On peut ainsi dégager une propriété du cerf-volant :
L'axe de symétrie du cerf-volant est médiatrice d'une de ses diagonales.
En application de la propriété de conservation des angles par symétrie
orthogonale : les angles BAD et BCD ont même mesure.
Question ouverte : le cerf-volant est-il un losange ?
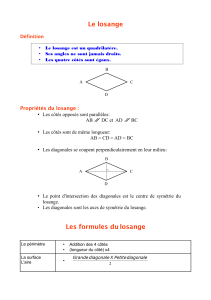
Le cerf-volant

Le losange
Mise en évidence de l'axe de symétrie (AC):
Utilisation de la propriété de conservation des longueurs par symétrie
orthogonale (AB' = B'C = AB = BC) pour identifier le losange (en lien avec le
cycle 3).
Un losange possède deux axes de symétrie.
En application de la propriété de conservation des mesures des angles par
symétrie orthogonale : les angles opposés ont même mesure.
Utilisation de la définition de la médiatrice d'un segment pour les segments
[BB'] et [AC] : les diagonales se coupent en leur milieu et sont
perpendiculaires.
Question ouverte :
Un losange est-il un cerf-volant particulier ?

L'intérêt de l'utilisation d'un logiciel de construction
géométrique
Rigueur dans le vocabulaire géométrique
Figures "propres"sur papier uni, construction facilitée par les
commandes
Aide au passage de la figure au texte (mémoire de la construction )
Identification des figures validée par la résistance à l'étirement
Passage du dessin à la notion de figure facilité ( aspect dynamique )
Construction rapide permettant d'entrer dans l'analyse et le raisonnement