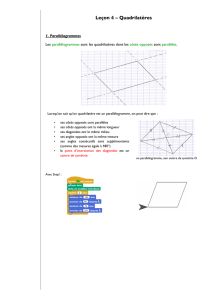
Le losange

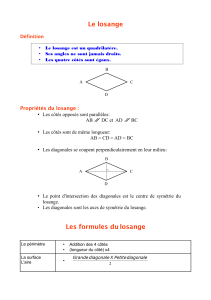
Le losange
Définition
Un losange est un quadrilatère qui a les côtés tous isométriques.
Représentation
Les droites remarquables
diagonales
médianes
Les diagonales sont deux droites
perpendiculaires qui partent d’un
somment vers le somment opposé et
qui se coupent en leur milieu.
Les médianes sont deux droites
sécantes en leur milieu qui partent du
milieu d’un côté vers le milieu du
côté opposé + les médianes sont
parallèle aux côtés qu’elles ne
coupent pas, et de même longueur
que les côtés.
base
hauteur
La hauteur, notée H, peut être mise
n’importe où. Elle doit être
perpendiculaire à la base et indique la
distance entre deux côtés parallèles
(qui sont les bases).
Les angles
Le losange a 4 angles dont la somme est égale à 360°. Les 2 angles opposés ont la même
amplitude. Le losange a une paire d’angles aigus qui sont opposés et une paire d’angles obtus
qui sont également opposés.
Le carré est un cas particulier qui a 4 angles droits.
angle aigu
angle obtus
De plus, les deux angles consécutifs (un aigu et un obtus) sont supplémentaires

Axes et centre de symétrie
axe de symétrie: grande diagonale
axe de symétrie: petite diagonale
Les axes de symétrie déterminent la symétrie
orthogonale ou encore la symétrie par rapport à
une droite.
 Centre de symétrie = intersections des
médianes et des diagonales
Un centre de symétrie détermine la symétrie
centrale ou encore la symétrie par rapport à un
point.
Les grandeurs associées
Aire du losange: on peut considérer le losange
comme la moitié d’un rectangle de longueur D et
de largeur d. Formule: d X D
2
Le périmètre d’un losange vaut la somme des longueurs de ses côtés, le losange ayant tous les
côtés isométriques, la formule donne 4L.

Constructions du losange
1) Croisement de deux bandes
Donnez les conditions de construction des
bandes: elles doivent avoir même largeur
2) Construction en utilisant la lettre graduée ou l’épreuve
 Tracer une grande diagonale.
 A la moitié, tracer la petite diagonale
perpendiculaire à la première. (les deux
diagonales doivent se couper on leur milieu)
Rejoindre les 4 extrémités.
3) Construction avec le compas
 Tracer une droite.
 Ouvrir le compas, choisir un point de la droite
et en tracer deux arcs de cercle passant par la
droite.
 Ouvrir le compas un peu plus.
 Placer le compas sur le point d’intersection de la droite et d’un arc de cercle et tracer deux
arcs de cercle en haut et en bas de la droite.
 Sans changer l’ouverture du compas, refaire la même démarche avec l’autre point
d’intersection.
Vous pourriez rechercher une ou deux variantes de ces constructions 2) et 3)
 Rejoindre les 4 points.

4) Le géoplan
Pouvez-vous imaginer
un losange sur géoplan
qui n’a pas de
diagonale horizontale?
5) Construction par assemblages de tiges articulées
 utilisation de pailles de même longueur!

6) Construction par assemblages de triangles
Qu’est ce qui motive ce choix ?
Il est surtout important de mentionner
les images importantes: un losange peut
être formé de
- 2 triangles isocèles isométriques
- 4 triangles rectangles isométriques
7) Construction par pliage (support: feuille ronde)
 Plier la feuille en 2
 Plier encore en 2
 Ouvrir la feuille
 Plier une moitié en bas de façon qu’elle touche la droite horizontale
 Refaire avec celle d’en haut
 Indiquer les 4 points déterminant les sommets
 Plier de façon quel les points de deux côtés adjacents deviennent les sommets