I- Triangles II- Quadrilatères

Classe de sixième Symétrie axiale et figures particulières
I- Triangles
a) Triangles isocèles
Propriété :
Un triangle isocèle a un axe de symétrie : la médiatrice de sa base.
Exemple :
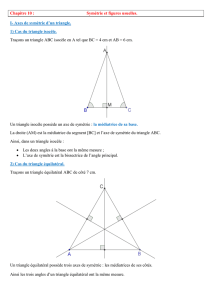
ABM est un triangle isocèle en M.
Donc la médiatrice de [AB] est l'axe de symétrie d u triangle.
Propriété :
Si un triangle est isocèle, alors la médiatrice de la base est aussi la bissectrice de l'angle principal.
Propriété :
Dans un triangle isocèle, les angles à la base sont de même mesure.
b) Triangles équilatéraux
Propriété :
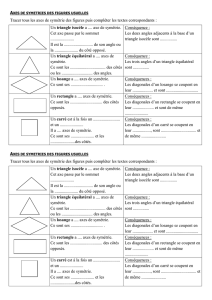
Dans un triangle équilatéral, les trois angles ont la même mesure.
Chaque angle mesure 60°.
Propriété :
Un triangle équilatéral a trois axes de symétrie : les médiatrices de ses côtés.
II- Quadrilatères
a) Cerf-volant
Définition :
Un cerf-volant est un quadrilatère qui a deux côtés consécutifs de
même longueur et les deux autres côtés de même longueur aussi.
Propriété :
Un cerf-volant a ses diagonales perpendiculaires
Un cerf-volant a une de ses diagonales pour axe de symétrie
Deux angles opposés d'un cerf-volant sont de même mesure.
Exemple :
ANBM est un cerf-volant. Le segment [MN] est l'axe de symétrie de cette figure.
Propriété pour identifier :
Si un quadrilatère a ses diagonales perpendiculaires, alors c'est un cerf-volant.
A
B
M
(d)
I
A
B
M
N
I

b) Losange
Propriétés :
Un losange a ses diagonales perpendiculaires et de même milieu.
Les diagonales d'un losange sont ses axes de symétrie.
Les angles opposés d'un losange sont de même mesure deux à deux.
Exemple :
ABCD est un losange. Les diagonales [AC] et [BD] sont perpendiculaires
et se coupent en leur milieu.
Propriété pour identifier !
Si un quadrilatère a ses diagonales perpendiculaires et qui se coupent en leur milieu, alors c'est un
losange.
c) Rectangle
Propriétés :
Un rectangle a ses diagonales qui se coupent en leur milieu et de même longueur.
Les médiatrices des côtés d'un rectangle sont ses axes de symétrie.
Exemple :
ABCD est un rectangle.
Ses diagonales sont de même longueur et se
coupent en leur milieu I.
Propriété pour identifier :
Si un quadrilatère a ses diagonales de même longueur et qui se coupent en leur milieu, alors c'est un
rectangle.
d) Carré
Propriétés :
Un carré a ses diagonales perpendiculaires, de même longueur et qui se coupent en leur milieu.
Les diagonales et les médiatrices des côtés du carré sont ses axes de symétrie.
Propriété pour identifier :
Si un quadrilatère a ses diagonales de même longueur,
perpendiculaires et qui se coupent en leur milieu, alors c'est
un carré.
C
D
B
A I
AB
C
D
I
A B
CD
O