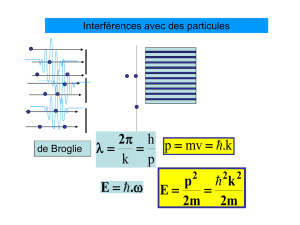
Interférences avec des particules

Troisième cours de physique

Etat quantique
stationnaire
Rappels
Paquet d’ondes 
Interférences avec
faisceau de particules
Equation de
Schrödinger
fonction du
temps
Interprétation
probabiliste de Origine physique de la
quantification
Quantification de l’énergie de
la particule
Exemple: Particule dans un
puits de potentiel infini
Equation de Schrödinger
indépendante du temps
+ Conditions aux limites
Correspondance de
De Broglie

k.k
h
p
h
2
paquet d’onde probabilité de présence
de la particule ponctuelle.
Interférences particule paquet d’onde
Ψ
Rappels
p
.E

Interférences avec des particules
(animation)

Interférences avec des particules
(animation)