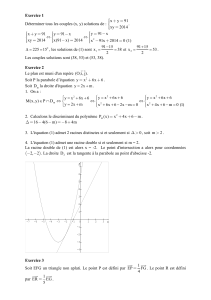
Exercices 1

LGL Cours de Mathématiques 2004
____________________________________________________________________________________________
____________________________________________________________________________________________
Beran Equations de droites - 1 -
Exercices sur les équations cartésiennes de droites
1) Soient les points A(-2;1) et B(1;-2) donnés dans un repère orthonormé (r.o.n.) )j;i;O(
G
G
(unité: 1cm).
Déterminer une équation cartésienne de la droite AB.
2) Soient les points
(
)
2; 1C
−
et 1
5; 2 D
donnés dans un repère orthonormé (r.o.n.) ()j;i;O
G
G
(unité: 1cm).
Déterminer une équation cartésienne de la droite CD.
3) Soient le point E(-2;3) et le vecteur directeur donnés dans un r.o.n. (
1
2
u
G)j;i;O
G
G
(unité: 1cm). Déterminer
une équation cartésienne de la droite
(
)
;dEu
G
.
4) Soient les points
(
)
1; 2−A,
(
)
0;5B et
(
)
3; 1C
−
donnés dans r.o.n. ()j;i;O
G
G
(unité: 1cm). Déterminer une
équation cartésienne de la droite AG, sachant que G est le centre de gravité du triangle ABC.
5) Soient les points
(
)
2; 4−A,
(
)
3; 1B− et
(
)
1; 7C− donnés dans r.o.n. )j;i;O(
G
G
(unité: 1cm). Déterminer une
équation cartésienne de chacune des trois médianes du triangle ABC.
6) Soient les points
(
)
1; 3A,
(
)
5; 2B−− et
(
)
3; 4C− donnés dans r.o.n. )j;i;O(
G
G
(unité: 1cm). Déterminer une
équation cartésienne de chacune des trois droites suivantes:
JJ
i)
(
)
1;dABC
JG
JJJG
ii)
(
)
2;dBAC
JJJG
iii)
(
)
3;dCAB
7) Soit la droite d d'équation: 05y3x2d
=
+
+≡ .
i) Déterminer un vecteur directeur de cette droite d
ii) Déterminer un point A de cette droite d
iii) Construire cette droite dans un r.o.n. ()j;i;O
G
G
(unité: 1cm)
8) Soient les points A(0;-1) et B(2;3) donnés dans r.o.n. ()j;i;O
G
G
(unité: 1cm). Déterminer une équation
cartésienne de la droite AB
9) Soient le point 
−4
3
;
2
1
C et le vecteur directeur u donnés dans un r.o.n.
9
10
G)j;i;O(
G
G
(unité: 1cm).
Déterminer une équation cartésienne de la droite )u;C(d
G
.
10) Soient les points A(-11;4) et B(2002;4) donnés dans un r.o.n. )j;i;O(
G
G
(unité: 1cm). Déterminer une équation
cartésienne de la droite AB
11) Soit le point C(-1;-2) donné dans un r.o.n. )j;i;O(
G
G
(unité: 1cm). Déterminer une équation cartésienne de la
droite CC' sachant que C
[]
C;Omil'=

LGL Cours de Mathématiques 2004
____________________________________________________________________________________________
____________________________________________________________________________________________
Beran Equations de droites - 2 -
12) Soient le point C(4;-1) et le vecteur directeur j
3
5
i
2
1
u
G
G
G
+−= donnés dans un r.o.n. )j;i;O(
G
G
(unité: 1cm).
Déterminer une équation cartésienne de la droite )u;C(d
G
.
13) Soient les points A(3;-2), B(1;4) et C(-3;-4) donnés dans r.o.n. )j;i;O(
G
G
(unité: 1cm). Déterminer une
équation cartésienne de la droite AA', sachant que A' est le milieu du segment [BC].
14) Soit la droite d d'équation: 04yx3d
=
−−≡ .
 Déterminer un vecteur directeur de cette droite d
 Déterminer un point A de cette droite d
 Construire cette droite dans un r.o.n. )j;i;O(
G
G
(unité: 1cm)
15) Soit la droite d d'équation: 01y
5
1
x
5
2
d=++≡ .
 Déterminer un vecteur directeur de cette droite d
 Déterminer un point A de cette droite d
 Construire cette droite dans un r.o.n. )j;i;O(
G
G
(unité: 1cm)
16) Soient le point A(1;2) et la droite d d'équation: d011y5x2
=
+
−
≡
donnés dans un r.o.n. ()j;i;O
G
G
.
Déterminer une équation cartésienne de la droite d' passant par A et parallèle à la droite d.
17) Soient les points A(7;3), B(2;1) et C(3;y) donnés dans r.o.n. )j;i;O(
G
G
(unité: 1cm).
 Déterminer l'ordonnée y du point C pour que C soit un point de la droite AB.
18) Soient les points A(1;2), B(5;-1) et C(-3;2) donnés dans r.o.n. )j;i;O(
G
G
(unité: 1cm).
 Déterminer une équation cartésienne de la droite AB.
 Déterminer une équation cartésienne de la droite d passant par C et d // AB .
 Déterminer la coordonnée du point D, sachant que ABCD est un parallélogramme.
 Contrôler que D est un point de la droite d.

LGL Cours de Mathématiques 2004
____________________________________________________________________________________________
____________________________________________________________________________________________
Beran Equations de droites - 3 -
Solutions des exercices:
1) 01yxAB =
+
+≡
2) 04y2xCD =−−≡
3) 08y2xd =
+
−≡
4) 2
2; 2 0
3
GAGy
 ≡−=
5)
(
)
'1;3 3 10 0
A
Amedxy≡+ − =
311
'; 13930
22 B
Bmedxy
−≡+
 0
−=
13
'; 11310
22 C
Cmedxy
 ≡+−=
 0
0
6)
1
230
6
BC d x y
 ≡−=
JJJG
2
413 0
1
AC d x y
−
 ≡++ =
JJJG
3
65639
5
AB d x y
−
 ≡−+=
−
JJJG
7) (un exemple possible)
3(2; 3)
2
vA
−
 −
G
8) 01yx2AB =−−≡
9) 012y10x9d =+−≡
10) 4yAB =≡
11) 0yx2'CC)1;
2
1
('C =−≡−−
12) 2yAG)2;
3
2
(G =≡−
13) 037y3x10d
3
5
2
1
u=−+≡
−
G
14) '( 1;0) ' 2 1 0
AAAxy−≡++=
15) )4;0(A
3
1
v−
G
16) )5;0(A
2
1
v05yx2d −
−
=++≡ G
17) 08y5x2'd
2
5
v=+−≡
G
18) )
5
7
;3(C
5
7
y01y532AB)y;3(C01y5x2AB
2
5
AB →=⇒=+−⋅⇔∈=+−≡
−
−
→
19)
43 4 11 0 3 4 1 0 ( 7;5)
3
AB AB x y d x y D
→ ≡+−= ≡++= −
−
021210154)7(3d)5;7(D
!
=+−=+⋅+−⋅⇔∈−