La convection dans le manteau terrestre - Seismo@School

La convection dans le manteau terrestre
La convection dans le manteau terrestre
Par Frédéric Deschamps (ETH Zürich) Résumé
La convection thermique est un mode de transfert de la chaleur par advection de matière. Elle
résulte de la croissance d’instabilités générées par des variations latérales de température. La
croissance de telles instabilités dans un fluide est contrôlée par les propriétés du fluide, la
géométrie du système, et la différence de température entre la base et le sommet du système.
Le manteau terrestre est instable vis-à-vis de la convection, ce qui, à l’échelle globale, induit la
formation de grands courants de convection. Ces mouvements sont responsables de la
Tectonique des Plaques. Au niveau des zones de subduction, ils se manifestent par le
plongement et le recyclage de croûte océanique dans le manteau profond. En première
approximation, la convection du manteau terrestre est assez bien décrite par des modèles
numériques et analogiques simples. Cependant, pour expliquer plus finement les observables
géophysiques disponibles, il est nécessaire de développer des modèles plus complexes qui
tiennent compte des variations des propriétés des roches du manteau terrestre avec la
température, la pression, et la composition. Table des matières
Un peu d’histoire Définitions et principes Un modèle simple et bien compris : la convection de
Rayleigh-Bénard Convection dans le manteau
terrestre Travaux dirigés Quelque
s liens utiles
Un peu d’histoire
Premières hypothèses. La théorie de la tectonique des plaques ne s’est pas imposée comme
une évidence parmi les géophysiciens et les géologues. Ses prémices furent posés en 1912
avec la dérive des continents d’Alfred Wegener, mais elle ne fut majoritairement acceptée qu’à
la fin des années 60. L’un des arguments opposés à Wegener était l’absence d’un moteur fiable
pour entretenir le mouvement des plaques. Wegener invoquait des forces dérivées de la
rotation terrestre, hypothèse peut convaincante si l’on considère la masse continentale qu’il
était nécessaire de déplacer. En 1945, Arthur Holmes propose une explication plus
satisfaisante : c’est un mouvement de convection global du manteau terrestre (c’est-à-dire
l’enveloppe située entre 50 et 2890 km de profondeur) qui permet d’entretenir le mouvement
des plaques en surface (Figure 1).
1 / 15

La convection dans le manteau terrestre
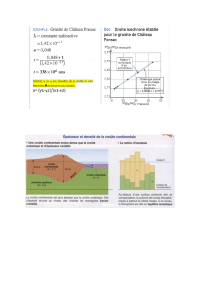
Figure 1. Le modèle proposé par Holmes (1945) pour expliquer la Tectonique des Plaques. (a)La convection dans le manteau terrestre induit des tensions qui fracturent cette croûte encertains endroits. (b) De la croûte océanique est créée au niveau des dorsales océaniques,parcristallisation de magma issu du manteau. La convection est également responsable de ladérive des plaques océaniques et continentales, et de leur recyclage au niveau des zones desubduction. Les années 60 et la Tectonique des Plaques. A partir de 1960, la tectonique desplaques apparaît être la meilleure explication aux variations du champ magnétique fossileenregistrées par les roches des planchers océaniques et à la distribution de la sismicitémondiale. La convection est de nouveau mise en avant comme moteur de la tectonique desplaques. Keith Runcorn, notamment, utilise la théorie de Rayleigh-Bénard pour montrer que lemanteau terrestre doit être animé de mouvements convectifs (on dit aussi qu’il est instablevis-à-vis de la convection), pourvu que sa viscosité soit inférieure à 10
25
Pas. Les calculs de Haskell, dans les années 30, indiquent justement que la viscosité dumanteau est de l’ordre de 10
21
-10
22
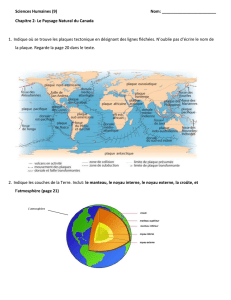
Pas. Dans cette hypothèse, des courants ascendants apportent du matériau nouveau au niveaudes dorsales océaniques. Ce matériau est ensuite entraîné loin des dorsales, se refroidi, avantde replonger dans le manteau au niveau des zones de subduction. Tuzo Wilson se placeégalement dans l’hypothèse d’une convection mantellique pour apporter une explication auvolcanisme intraplaque (aussi appelé volcanisme de point chaud, correspondant à des volcansqui ne sont pas situés pas sur des frontières de plaques tectoniques ; c’est par exemple le casdes îles Hawaii ou de l’île de la Réunion): une source magmatique issue du manteau profond etfixe par rapport à l'écoulement du manteau se manifeste en surface par la formation d'unechaîne volcanique (Figure 2).
Figure 2. La formation des chaînes volcaniques intra-plaques, d’après Wilson (1963). (a) Coupedu manteau. (b) Trace de la chaîne volcanique en surface. Modéles numériques etanalogiques. A partir des années70, les géophysiciens se sont attachés à modéliser la convection du manteau terrestre enlaboratoire, en se basant sur des méthodes numériques (résolution des équations de laconvection à l’aide d’ordinateurs) et des expériences analogiques (reproduction de laconvection dans des cuves de petite dimension). Ces modèles sont nécessairement simplifiéset ne tiennent pas compte de toutes les complexités liées au manteau terrestre. Toutefois, leursrésultats confortent l’hypothèse que les transferts de chaleur et de masse dans le manteauterrestre se font par convection. Les premiers modèles numériques apparaissent dans lesannées 70. Ils sont très simples (calculs en 2D seulement, fluide isovisqueux, …), mais dansleurs grandes lignes ils expliquent relativement bien les observations de surface telles que leflux de chaleur issu du manteau et la vitesse des plaques. Les premières expériencesanalogiques ont été conduites dès la fin des années 60, et se sont en particulier attachées àdécrire la géométrie de l’écoulement en fonction des propriétés du fluide et du système. Depuisces premier modèles, l’accroissement de la puissance de calcul et l’amélioration desalgorithmes et des méthodes numériques ont permis de construire des modèles de plus en pluscomplexes tenant compte de paramètres important, notamment la rhéologie (variations deviscosité) des roches du manteau, la production de chaleur par radioactivité, et la présence detransitions de phase. Les modèles (numériques et analogiques) actuels développés par lesgéophysiciens s’attachent en particulier à décrire plus finement le mode de convection dumanteau (c’est-à-dire à en identifier les paramètres de contrôle), de façon à expliquerl’ensemble des observables géophysiques disponibles, notamment les observationssismologiques. A ce jour, le mode de convection du manteau terrestre ne fait toujours pasl’objet d’un large consensus.
2 / 15

La convection dans le manteau terrestre
3 / 15

La convection dans le manteau terrestre
Figure 3. Trois générations de modèles numériques (colonne de gauche). En haut, modèle2D-Cartésien pour un fluide isovisqueux par Dan McKenzie et collaborateurs (1974). Lavignette de gauche représente la distribution de température, et celle de droite la fonction decourant. Au milieu, modèle en 3D-Cartésien avec chauffage mixte par Christophe Sotin etcollaborateurs (1996). Les isosurfaces bleues montrent les courants froids descendant, et lesisosurfaces oranges représentent les panaches chauds. En bas, modèle en géométriesphérique pour un fluide isovisqueux par Paul Tackley et collaborateurs (2010). La vignette degauche montrent deux isosurfaces (en bleu les courants froids descendant, en rouge lespanaches chauds ascendants), et celle de gauche la distribution de température. Modèlesanalogiques (colonne de droite). En haut, expériences 3D de type Rayleigh-Bénard par DavidWhite (1988). La prise de vue montre la surface du fluide et montre la géométrieapproximativement hexagonale des cellules de convection obtenue dans ce cas. En bas,convection thermo-chimique en 3D par Anne Davaille (1999). Une couche de fluide plus denseest initialement disposée dans la partie inférieure de la boîte. Au bout d’un certain temps, cettecouche devient instable, et piour certaines valeurs du rapport de densité entre les matériauxdense et régulier, de grand dômes thermo-chimiques oscillent sur toute l’épaisseur de la boîte.
Back
Définitions et principes
Le phénomène de convection est généré par le développement d'instabilités dans un milieu
initialement stable, auquel on superpose à un instant donné une petite perturbation. La nature
de la perturbation n'est pas unique et conduit à différents types de convection: variations de la
vitesse angulaire de rotation (instabilité de Taylor-Couette), de la composition chimique, ou de
la température. Dans ces deux derniers cas, le moteur de la convection est la poussée
d'Archimède, c’est-à-dire des variations latérales de densité induites par les variations de
composition chimique ou de température. Il existe plusieurs freins au développement des
instabilités ainsi initiées, notamment la diffusion thermique, qui tend à homogénéiser la
température du milieu, et la viscosité du fluide, qui augmente les forces de frottement. La
capacité de la convection à surmonter ces difficultés est exprimée à l'aide de nombres sans
dimensions, eux-mêmes définis à partir des propriétés physiques et géométriques du système.
Convection thermique
. Lorsqu’elle est chauffée, une particule de fluide devient moins dense que ses voisines, ce qui
induit des variations latérales de pression et de contrainte, donc une situation instable d’un
point de vu dynamique qui conduit la particule chaude à entamer une ascension. A l’inverse,
lorsqu’elle est refroidie, une particule devient plus dense que ces voisines et va entamer une
descente. Globalement, les variations latérales de densité (ici, dues à des variations latérales
de température) induisent un mouvement d’ensemble du fluide. Dans un système chauffé à sa
base et refroidi en surface, le matériau situé à la base se charge en chaleur, remonte en
surface où il cède la chaleur qu’il a accumulé et se refroidi, avant de replonger vers la base du
4 / 15

La convection dans le manteau terrestre
système (c’est par exemple ce qu’il se passe dans une casserole rempli d’eau que l’on met sur
le feu). La convection thermique constitue donc un mode de transfert de la chaleur par
advection de matière.
Une étude plus complète de la convection thermique nécessite de résoudre trois équations,
chacune étant associée à une loi de conservation : conservation de la quantité de mouvement
(pour calculer le champ de vitesse, i.e., les trajectoires des particules de fluide), conservation
de l’énergie (pour calculer la répartition de température), et conservation de la masse.
L’équation qui décrit la conservation de la quantité de mouvement (et qui n’est autre que la
relation fondamentale de la dynamique appliquée à un milieu continu) est parfois appelée
équation de Navier-Stokes. Il est d’usage de négliger l’accélération des particules de fluide, qui
est de fait très petite en comparaison des autres termes (la force de gravité, les variations de
pression, et les contraintes visqueuses). Cela simplifie énormément le problème, mais pas
suffisamment pour pouvoir le résoudre analytiquement. Dans certains cas simples (p.e., la
convection de Rayleigh-Bénard), il est possible de définir analytiquement des critères de
stabilité et des lois d’échelles pour les certaines observables (vitesse horizontale et flux de
chaleur moyens en surface). Toutefois, pour calculer l’écoulement et la distribution de
température, il est nécessaire de résoudre les équations de la convection numériquement à
l’aide d’ordinateurs.
Convection thermique vs conduction.
Pour que la particule chauffée puisse continuer son ascension (et, éventuellement, atteindre la
surface), elle ne doit pas échanger trop de chaleur avec ces voisines successives sur son trajet.
Autrement dit, la conduction thermique (un autre mode de transfert de la chaleur) ne doit pas
être trop élevée. Plus précisément, le temps caractéristique de diffusion de la chaleur doit être
est très supérieur au temps caractéristique de diffusion de la quantité de mouvement (le rapport
entre ces deux temps caractéristiques est mesuré par le nombre de Prandtl). Si tel est le cas la
particule n’aura pas le temps d’échanger de chaleur avec ses voisines, et pourra donc
conserver jusqu’en surface la chaleur qu’elle a emmagasiné. La capacité à conduire la chaleur
dépend bien sûr du matériau, certain matériaux (par exemple, les métaux) conduisant bien
mieux la chaleur que d’autre (par exemple le bois). Les roches composant le manteau terrestre
conduisent particulièrement mal la chaleur. Propriété Symbol Valeur Unité
Epaisseur D 2891 km
Accélération de la gravitég 9.81 m/s 2
Densité ρ 3500 kg/m 3
Viscosité μ 5.0×10 21 Pa.s
Expansion thermique α 3.0×10 -5 1/K
Conductivité thermique k 3.0 W/m/K
Diffusivité thermique κ 10 -6 m2/s
Production de chaleur interne par radioactivitéH 6.0×10 -12 W/kg
Contraste vertical de températureΔT 2500 K
Table 1. Quelques propriétés moyennes du manteau terrestre. Pour la
pluparts, ces valeurs sont des ordres de grandeurs, et restent assez mal
contraintes. L’épaisseur du manteau et l’accélération de la gravité sont très
bien connus. En revanche, le contraste de température est lui très mal
contraints, et se situe quelque part entre 2000 et 3000 K. La viscosité varie
5 / 15