TP 9 physique : Terminale Les lois de NEWTON Objectifs.

TP 9 physique : Terminale Les lois de NEWTON
Objectifs.
- S’approprier la notion d’accélération et comprendre l’intérêt de lui associer un vecteur.
- Construire un vecteur accélération.
- Etablir une relation quantitative entre la résultante des forces extérieures appliquées à un
mobile et l’accélération.
I. Du vecteur vitesse au vecteur accélération : activité de questionnement 1 livre Hatier page 194
1. Cas d’un mouvement rectiligne.
Dispositif :
Tableau de mesures :
t ( s ) x ( cm ) v ( m.s-1 ) a ( m.s-2 )
0,00 0,0 0,30
0,04 1,3
0,08 2,9
0,12 4,8
0,16 7,0
0,20 9,4
0,24 12,1
0,28 15,1
0,32 18,3
0,36 21,8
0,40 25,6 0,98
Exploitation : répondre aux questions a, b et c du livre p 194.
2. Cas d’un mouvement quelconque
II. Des forces à l’accélération : Activité expérimentale 2 livre Hatier p 195
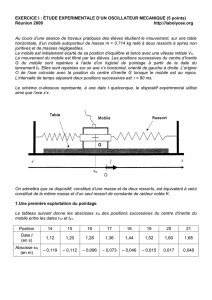
Montage expérimental : mobile autoporteur sur table à coussin d’air.
Exploitation : Utiliser l’enregistrement ci-contre pour répondre aux questions a, b, c, d, e et f du
livre p 195.
Pour les plus rapides : proposer une méthode pour mesurer la constante de raideur k du ressort
utilisé dans l’expérience.
Exploitation :
répondre aux questions a, b c et d du
livre p 194.

Reproduction à l’échelle 1/2 de l’enregistrement du
mouvement du centre d’inertie d’un mobile.
Le mobile est relié à un ressort. L’autre extrémité du ressort
est fixe (point O). Quand le ressort n’est ni étiré, ni
comprimé le centre d’inertie du mobile est situé au point G.
Masse du mobile : m = 723 g
Constante de raideur du ressort k = 5,2 N.m-1
Durée entre 2 positions successives du mobile : τ = 0,06 s

CORRECTION
c.
d. Les vecteurs vitesses appartiennent au plan du mouvement qui contient la trajectoire. Il en est
de même de la différence de ces deux vecteurs vitesses et donc du vecteur accélération.
Le représentant de v
r
∆
a pour longueur 2,65 cm.
Une mesure de la distance parcourue pour aller de
M1 à M3, permet de déterminer l’échelle des
vecteurs vitesses :
v2 = (0,7+0,8).10-2 / 2 x 0,04 = 0,19 m.s-1 ;
longueur de v2 : 1,5 cm
Echelle des vecteurs vitesses :
1 cm correspond à 0,19 /1,5 = 0,13 m.s-1
v
r
∆
a donc pour valeur 0,34 m.s-1
a
r
3 a pour valeur 0,34 / 2 x 0,08 = 4,3 m.s-2

II. Des forces à l’accélération
Données : m = 723 g ; τ = 0,06 s ; k = 5,2 N.m-1 ;
Echelle du document : 1/2 ; OG = 17 cm ;
a. F
r
=
T
r
Calcul de la norme de
T
r
: T = k . (l – l0) = k . (OG3 – OG0) = 5,2 x (15,6 – 8,5) x 2 x 10-2 = 0,74 N
Représentation de
T
r
: échelle 1 cm pour 0,1 N
b. a
r
3 = ( v
r
4 - v
r
2) / 2 . τ
a
3 = ∆v / 2 τ
c.
G2G3= 1,6 cm ; G3G5 = 1,65 cm
V2 = (1,6 x 2) / 2 x 0,06 = 26,6 cm.s-1 ;
V4 = (1.65 x 2) / 2 x 0,06 = 27,5 cm.s-1 .
Tracé des vecteurs vitesses :
Echelle : 1 cm pour 5 cm.s-1
Expérimentalement : ∆v = 2,55 x 5 cm.s-1
Accélération : a3 = ∆v / 2 τ = 2,55 x 5 / 2 x 0,06 = 106 cm.s-1 = 1,06 m.s-2
Tracé du vecteur accélération :
Echelle : 1 cm pour 0,2 cm.s-2
d. La résultante des forces appliquées au mobile et le vecteur accélération de soncentre d’inertie ont bien
la même direction et le même sens.
e. F / a3 = 0,74 / 1,06 = 0,70 kg
La valeur trouvée correspond à la masse du mobile.
f. F
r
= m a
r
3
Dans un référentiel galiléen, la résultante des forces appliquées à un solide est égale au
produit de sa masse par l’accélération de son centre d’inertie.
Rem : Les grandeurs F et ma sont sensiblement égales à 4% près.
Pour les plus rapides :
Méthode pour déterminer la constante de raideur k du ressort utilisé :
- mesure de la longueur à vide du ressort l0 suspendu à un support
- suspendre une masse de 50 g à l’extrémité du ressort
- mesurer la longueur du ressort l
- en déduire k : k = mg / (l - l0)
Matériel : au bureau
• Table à coussin d’air et accessoires
• Mobile autoporteur + ressort + ficelle
• Feuille A3
• Balance
• Potence + masses marquées

Reproduction à l’échelle 1/2 de l’enregistrement du
mouvement du centre d’inertie d’un mobile.
Le mobile est relié à un ressort. L’autre extrémité du ressort
est fixe (point O). Quand le ressort n’est ni étiré, ni
comprimé le centre d’inertie du mobile est situé au point G.
Masse du mobile : m = 723 g
Constante de raideur du ressort k = 5,2 N.m-1
Durée entre 2 positions successives du mobile : τ = 0,06 s