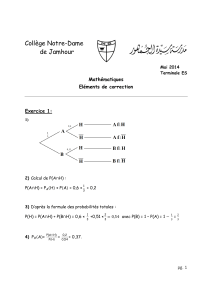
ϕi χp χp

CALCULS SUR LES MOLECULES
Nous allons maintenant voir plusieurs méthodes de calcul ayant pour but la description et
la prédiction des propriétés de molécules et de liaisons chimiques. Le problème de la
formation et du bris des liaisons est toujours le problème central de la chimie quantique.
L'approximation LCAO
Les équations de Hartree-Fock sont des équations intégro-différentielles, une classe
d'équations qui est difficile à résoudre. Pour des atomes, ou pour des molécules linéaires,
on peut profiter de la symétrie élévée, et des solutions numériques quasi-exactes sont
maintenant disponibles. Par contre, la vaste majorité de calculs sur les molécules se
servent d'un développement des orbitales moléculaire dans une base de fonctions connues
(comme on a vu dans l'exemple de l'atome d'hydrogène calculé avec des fonctions
gaussiennes). On écrit
ϕ
i(1) =cpi
χ
p(1)
p
∑
où
χ
p(1) peut être en principe n'importe quel ensemble (en principe complet) de
fonctions acceptables.
Très souvent on choisit des fonctions pour profiter du fait que les molécules renferment
des atomes qui, tout en étant déformés (perturbés) par leur insertion dans la molécule
sont, tout-de même, reconnaissables comme les atomes de départ. On choisit, donc, des
fonctions "centrées" sur les différents noyaux de la molécule (ayant les noyaux comme
origines du système des coordonnées locales). On parle de l'approximation LCAO - MO
(Linear Combination of Atomic Orbitals - Molecular Orbitals); CLOA - OM
(Combinaisons Linéaires d'Orbitales Atomiques - Orbitales Moléculaires).
Prenons la molécule H2 comme exemple (nous allons beaucoup travailler avec cette
molécule dans les prochains cours). Définissons les coordonnées
1

1a
r
G 1b
r
G
ab
R
G
2a
r
G 2b
r
G
a b
1
2
Maintenant, si un électron est proche du noyau a, il va sentir, comme potentiel,
surtout l'attraction du noyau a. Par conséquent, sa fonction d'onde devrait se
ressembler à une fonction d'onde pour un atome d'hydrogène situé à la position du
noyau a. Nous écrivons
1sa(1) =Ne
−
r
1a
De même, si l'électron est proche du noyau b
1s
b
(1) =Ne
−
r
1b
Notre fonction LCAO-MO est une combinaison linéaire de ces deux fonctions
2

ϕ
(1)=N' c11sa(1)
{
}
c21sb(1)
+
=N' c1e−r1a +c2e−r1b
{
}
Pour l'état fondamental, c1 = c2
ϕ
=N' 1sa+1sb
(
)
=N(a+b)
et nous avons une fonction moléculaire qui est piquée aux deux noyaux.
a
b
Dans le cas générale un MO aura un pic à chaque noyau de la molécule.
En 1951, Roothaan a montré comment combiner l'approximation LCAO avec la méthode
de Hartree-Fock. La très grande majorité des calculs HF effectués aujourd'hui se servent
3

de ce formalisme. On doit résoudre une équation séculaire (il s'agit d'un calcul
variationel linéaire)
F11−
(
ε
)
c1+F12
(
)
−
ε
S12 c2
+
... F
1n
(
)
−
ε
S1n cn=0
F21−
ε S21
(
)
c1+F22 − ε
(
)
c2+... F2n − ε S2n
(
)
cn=0
MM
(Fnn −
ε )cn=0
Où les éléments de la matrice de Fock sont donnés par
Fpq =
χ
pˆ
F
χ
q
= χ
p−1
2∇2−ZM
r1M
M
∑
χ q+Prs
rs
∑pr / qs
où Prs =2c
ri
occ
∑csi
et pr qs = χ
p
*
∫∫ (1)
χ
r
*(2) 1
r12
χ
q(1)
χ
s(2)dv1dv2
Pour former la matrice de Fock, il faut connaître les coefficients c, c'est-à-dire les
solutions du problème, donc, encore une fois, une solution itérative s'impose. Les
intégrales < pq | rs > sont des intégrales biélectroniques, impliquant des fonctions de base
associées avec jusqu'à quatre noyaux différents. Leur calcul efficace représente un des
grands défis (et un des grands succès) de la chimie quantique. Le nombre de ces
intégrales augmente rapidement (comme la quatrième puissance) avec la taille de la base.
Par conséquent, les grosses molécules sont beaucoup plus difficiles à traiter que les
petites. Dans une première analyse, le nombre d'intégrales biélectronique est égal à 1/8
n4, où n est le nombre de fonctions dans la base. Le tableau suivant démontre la
croissance du nombre d'intégrales avec n.
4

n nombre approx. d'intégrales
10 1000
50 5 x 105
100 107
500 5 x 109
1000 1011
5000 1014
(1 Mégabyte = 105 intégrales. 1 Gigabyte = 108 intégrales)
Évidemment le calcul, le stockage et la manipulation d'un tel nombre d'intégrales
nécessite des techniques spéciales....
Un ordinateur avec
• 1000 Gb de disque dure
• 70 CPU
• 100 Gb de mémoire
5