Chapitre II : Interférences lumineuses 1. Généralités

Spéciale PSI - Cours "Optique ondulatoire" 1
Interférences
Chapitre II : Interférences lumineuses
Objectif :
•Dénir le phénomène d’interférence.
•Conditions d’obtention d’interférence en optique.
1. Généralités
1.1. Représentation scalaire des ondes (rappels)
Selon la nature de la grandeur vibratoire, les ondes peuvent être :
•scalaires, comme par exemple les ondes acoustiques de pression,
•vectorielles, comme les ondes électromagnétiques.
Dans ce dernier cas, la superposition de deux ou plusieurs ondes en un point conduit à composer des champs vectoriels
n’ayant en général pas la même direction. Par exemple le champ électrique résultant s’écrirait :  E= E1+
E2
On rappelle que dans un grand nombre de situations, l’intensité lumineuse, due à la superposition de plusieurs ondes élec-
tromagnétiques, peut être déterminée au moyen d’un modèle simpli'é, où le champ électrique est associé à une grandeur
scalaire.
Cette approximation est justi'ée :
•dans le cas très fréquent d’ondes non polarisées dont les directions de propagation sont voisines ;
•pour des ondes polarisées dont on sait que les directions de polarisation sont voisines.
Il n’est alors plus nécessaire de garder à la grandeur vibratoire son caractère vectoriel et l’on adoptera une notation
scalaire pour la vibration lumineuse : en chaque point Mon associe à la lumière monochromatique une vibration scalaire,
appelé signal lumineux,dutype
s(M,t)=s0cos 
k.rt
ou en notation complexe
s(M,t)=s0exp i
k.rt
1.2. Interférence
Il y aura un phénomène d’interférence lorsque l’intensité de la superposition de plusieurs ondes n’est pas la somme des
intensités de chacune de ces ondes. Ce phénomène se produit dans une même région de l’espace (champ d’interférence)
où se superposent plusieurs ondes (nous nous limiterons dans ce chapitre au cas de deux ondes) qui possèdent la propriété
d’être à la fois :
•synchrones : c’est à dire avoir la même fréquence ,
•cohérentes : c’est à dire présenter un déphasage , en général variable selon le point de l’espace (point du champ
d’interférence) considéré, mais demeurant constant sur une durée au moins égale au temps de réponse Rdu
récepteur.
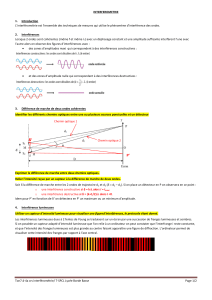
1.3. Exemple
Une bulle de savon éclairée en lumière naturelle (blanche) ré.échit une lumière dont la couleur dépend de l’épaisseur.

Optique ondulatoire. Chapitre II : Interférences lumineuses 2
2. Expression de l’intensité dans un phénomène d’interférence de deux ondes
2.1. Position du problème
Supposons qu’en un point Mdonné se superposent deux ondes satisfaisant aux conditions énoncées dans le paragraphe
précédent. En particulier les phases des deux sources, désignées par 01et 02sont supposées être indépendantes du temps
(sources cohérentes).
Les amplitudes de leurs vibrations respectives s’écrivent scalairement au point M, en regroupant sous la notation le
déphasage dû à la propagation avec la phase à l’origine de la source :
s1(M,t)=s01cos (01 +kr
1t)=s01cos (1t)
s2(M,t)=s02cos (02+kr
2t)=s02cos (2t)
S
1
S
2
r
1
r
2
M
Nous allons dans un premier temps e4ectuer le calcul détaillé de l’intensité lumineuse recueillie par un récepteur placé en
M, puis nous montrerons comment le résultat peut s’obtenir très rapidement en utilisant la notation complexe.
2.2. Calcul détaillé
Ecrivons les intensités lumineuses I1(M, t)et I2(M, t)que l’on obtiendrait au point Msi chacune des sources S1et S2émettait
seule (rappel : un récepteur lumineux détecte une intensité lumineuse correspondant à une intensité moyenne proportionnelle
à la valeur moyenne dans le temps du carré du signal lumineux (du champ électrique) :
I1(M)=Ks2
1(M,t)t=Ks
2
01 cos2(1t)t=1
2Ks
2
01
I2(M)=Ks2
2(M,t)t=Ks
2
02 cos2(1t)t=1
2Ks
2
02
Si les deux sources émettent simultanément, l’amplitude s(M,t)de la vibration résultante s’écrit :
s(M,t)=s1(M,t)+s2(M, t)
et donc :
[s(M,t)]2=[s1(M,t)+s2(M, t)]2=s2
1(M,t)+s2 2(M,t)+2s1(M, t)s2(M,t)
Le récepteur lumineux détecte alors une intensité lumineuse Iqui s’écrit, en posant =21,di4érence de phase que
présentent à tout instant les vibrations en M:
I(M)=Ks2(M,t)t=Ks2
1(M,t)+s2 2(M,t)+2s1(M, t)s2(M,t)t
=Ks2
1(M,t)t+Ks2 2(M,t)t+2Ks1(M,t)s2(M,t)t
=I1(M)+I2(M)+2Ks01s02 cos (1t)cos(2t)t
=I1(M)+I2(M)+2Ks01s02 cos (1t)cos(2t)t
=I1(M)+I2(M)+2Ks01s02 1
2cos (21)+1 2cos (1+22t)t
=I1(M)+I2(M)+2
I1(M)I2(M)cos (21)+cos(1+22t)t
=I1(M)+I2(M)+2
I1(M)I2(M)cos(21)

Optique ondulatoire. Chapitre II : Interférences lumineuses 3
On a donc
I=I1+I2+2
I1I2cos avec =21
Remarque : c’est lorsque nous écrivons que :
cos (21)t=cos (02+kr
201kr 1)t
=cos(02+kr
201kr 1)
qu’intervient la condition essentielle de cohérence des deux ondes.
2.3. Calcul rapide
La méthode utilisant la notation complexe présentée ci-après pour deux ondes reste bien sûr valable et encore
plus e*cace pour trois, Nou une in,nité d’ondes.
Dans le plan complexe, ou en représentation de Fresnel :
1
I
Axe origine des phases
2
I
I
2
1
s1(M,t)=s01 cos (01 +kr
1t)=s01 cos (1t)s1(M,t)=s01 exp [i(1t)] = s01 exp (i1) exp (it)
s2(M,t)=s02 cos (02 +kr
2t)=s02 cos (2t)s2(M,t)=s02 exp [i(2t)] = s02 exp (i2) exp (it)
L’intensité lumineuse donnée par un récepteur est proportionnelle à la valeur moyenne dans le temps du carré du signal
lumineux
I(M)=Ks2(M,t)t
Pour une onde monochromatique
I(M)=1
2Ks2
0
soit en notation complexe
I(M)=1
2Kss
Exercice n01 :Démontrer, en utilisant la notation complexe, qu’on retrouve bien le même résultat que précédement.
Remarque : On ne s’intéresse le plus souvent qu’aux variations de l’intensité lumineuse et la constante 1
2Kest ”oubliée”:
I(M)ss=[s01 exp (i1)+s02 exp (i2)] [s01 exp (i1)+s02 exp (i2)]=...
2.4. Cas particulier de deux ondes de même amplitude
Si les deux vibrations qui interfèrent ont la même amplitude s01 =s02 =s0on a I1=I2=I0et l’intensité totale est donnée
par :
I=2I0(1 + cos )
3. Description du champ d’interférences
Sans décrire en détail le champ d’interférences, nous le ferons plus loin dans le chapitre sur des cas particuliers, signalons dès
maintenant quelques points fondamentaux.

Optique ondulatoire. Chapitre II : Interférences lumineuses 4
3.1. Etat d’interférence, franges d’interférences
Le terme 2I1I2cos (M), caractéristique d’un phénomène d’interférences à deux ondes, s’appelle terme d’interférences.
La di4érence de phase (M)varie selon la position du point Mpuisque
(M)=(02 +kr
2)(01 +kr 1)
La valeur de (M)dé'nit l’état d’interférence des vibrations qui interfèrent. A un état d’interférence donné correspond
une intensité Iconstante et le lieu des points Mpour lesquels l’intensité I(M)garde une valeur constante est appelé frange
d’interférence :
(M)=cste état d’interférence constant frange d’interférence
Les valeurs remarquables de la di4érence de phase sont :
•(M)=2qavec qZcos (M)=1frange lumineuse (vibrations en phase) :
Imax =I1+I2+2
I1I2
•(M)=(2q+1)avec qZcos (M)=1frange sombre (vibrations en opposition de phase) :
Imin =I1+I22I1I2
Remarques :
1) Entre deux franges lumineuses (ou deux franges sombres) consécutives, (M)varie de 2.
2) Entre une frange lumineuse et une frange sombre adjacentes, (M)varie de .
3) Lorsqu’on se déplace dans le champ d’interférences, la conservation de l’énergie impose que la moyenne spatiale de
l’intensité soit égale à la somme des intensités que produiraient séparément les deux sources, les interférences ne faisant
que modi,er la répartition d’énergie :
I(M,t)M=I1+I2+2
I1I2cos ()M
=I1+I2+2
I1I2cos ()M
=I1+I2
3.2. Contraste (visibilité) des franges
3.2.1. Dé,nition
On dé'nit le contraste (visibilité) des franges par :
V=Imax Imin
Imax +Imin
•Lorsque l’intensité lumineuse minimale est nulle, les franges lumineuses se détachent sur un fond noir et sont alors
parfaitement observables : le contraste vaut 1.
•Lorsque l’intensité minimale n’est pas nulle, les franges lumineuses se détachent moins bien et le contraste est alors
inférieur à 1.
•A la limite où l’intensité minimale est égale à l’intensité maximale, on n’observe bien sûr plus de franges et le contraste
est alors nul.
3.2.2. Expression du contraste dans une interférence d’ondes d’intensités di/érentes
Avec les notations précédentes on a
I=I1+I2+2
I1I2cos ()=(I1+I2)(1+Vcos ()) avec V=2I1I2
I1+I2
On obtient alors les tracés suivants de l’intensité en fonction de pour di4érentes valeurs du contraste :

Optique ondulatoire. Chapitre II : Interférences lumineuses 5
0
4
2
2
4
I/I
0
0
4
2
2
4
I/I
0
V=1 V=0,4
Simulation (Maple)Simulation (Maple)
Exercice n02 :Démontrer les résultats précédents.
3.3. Expression du déphasage 
3.3.1. Di/érence de marche ”géométrique”
On rappelle que pour une onde monochromatique de pulsation et de longueur dans le vide 0,ladi4érence de phase dûe
à la propagation des ondes à tout instant entre les points Aet Bd’un même rayon lumineux est :
(AB)g´eo =2
0
(AB)
Utilisons cette relation pour exprimer g´eo(M)=(2(M)1(M))g´eo :
S1
S2
M
L’onde (1) est de la forme s1(M, t)=s01 cos (01 +kr
1t)=s01 cos (1t)et
S1M=2
0
(S1M)