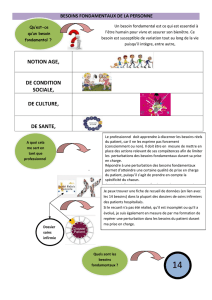
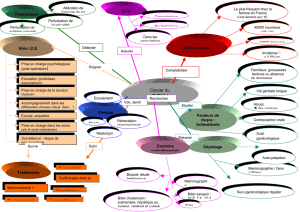
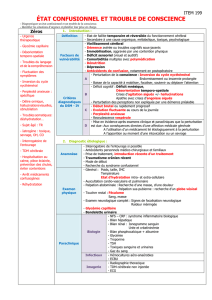
Physique quantique appliquée A Perturbation au 2nd ordre de l?état

Université Pierre et Marie Curie
M1 - MP051 Année 2009–2010
Physique quantique appliquée
TD n8 : Théorie des perturbations stationnaires (e¤et Stark)
On considère un atome d’Hydrogène - supposé sans spin et au repos - placé dans un champ électrique ! E
constant dont l’orientation est suivant le vecteur ! ez(
!
E
=E). On rappelle qu’en l’absence de champs
extérieurs, les niveaux d’énergie sont donnés par :
En=EI
n2avec n>1et EI= 13;6eV
Ils sont dégénérés n2fois et les états propres associés sont notés jnlmi. L’Hamiltonien de perturbation peut
alors s’écrire sous la forme :
W=e! r :! E=ezE
où zest l’opérateur position. Cet Hamiltonien induit une modi…cation des niveaux d’énergie En(e¤et Stark)
que l’on se propose d’étudier.
*******
A - Perturbation au 2nd ordre de l’état fondamental n= 1
A.1 Donner l’expression de la perturbation au 1er ordre E1du niveau n= 1.
A.2 Sachant que les états jnlmiont une parité bien dé…nie (ils sont soit pairs soit impairs sous inversion
spatiale), montrer que E1= 0. Conclusion.
A.3 Donner l’expression de la correction au 2nd ordre 2E1du niveau fondamental (en faisant apparaître
le facteur (eE)2=EI). De quel signe est-elle ?
A.4 On peut montrer que les éléments de matrice hnlmjWjn0l0m0isont nuls lorsque l+l0est pair (pour
des questions de parité) ou lorsque m6=m0(car Lzcommute avec W). Donner les 3 premiers termes de
l’expression de 2E1.
A.5 La somme des di¤érents termes de l’expression de 2E1conduit au résultat suivant :
2E1=1
2E2avec : = 18"0a3
0(polarisabilité)
où "0= 8;85:1012Kg1m3A2s4est la permittivité du vide et où a0= 5;3:1011mest le rayon de Bohr.
Quelle est la valeur de 2E1(en eV ) pour un champ électrique de 104V=cm ? Comparer cette valeur à l’écart
entre les niveaux E1et E2. Conclusion.
1

B - Perturbation du niveau n= 2 et levée de dégénérescence
B.1 Quelle est la dégénérescence du niveau n= 2 ? Quels sont les états associés ?
B.2 Sachant que seuls les 2éléments de matrice suivant sont non-nuls :
h200jWj210i=h210jWj200i= 3a0eE
déterminer les corrections du 1er ordre à l’énergie E2.
B.3 En combien de niveaux di¤érents se scinde le niveau n= 2 sous l’e¤et de W?
B.4 Quels sont les nouveaux états propres ?
*******
CORRECTION
*******
On considère un atome d’Hydrogène - supposé sans spin et au repos - placé dans un champ électrique ! E
constant dont l’orientation est suivant le vecteur ! ez(
!
E
=E). On rappelle qu’en l’absence de champs
extérieurs, les niveaux d’énergie sont donnés par :
En=EI
n2avec n>1et EI= 13;6eV
Ils sont dégénérés n2fois et les états propres associés sont notés jnlmi. L’Hamiltonien de perturbation peut
alors s’écrire sous la forme :
W=e! r :! E=ezE
où zest l’opérateur position. Cet Hamiltonien induit une modi…cation des niveaux d’énergie En(e¤et Stark)
que l’on se propose d’étudier.
*******
A - Perturbation au 2nd ordre de l’état fondamental n= 1
A.1 Donner l’expression de la perturbation au 1er ordre E1du niveau n= 1.
niveau n= 1 non-dégé
=)E1=h100jWj100i
2

A.2 Sachant que les états jnlmiont une parité bien dé…nie (ils sont soit pairs soit impairs sous inversion
spatiale), montrer que E1= 0. Conclusion.
E1=h100jWj100i=eE h100jbzj100i
h100jzj100i=Z+1
1
100 (z):z:100 (z):dz
avec 100 (z)la fonction d’onde associée au ket j100i.
D’où :
h100jzj100i=Z+1
1
zj100 (z)j2dz
Avec le changement de variable z! z, on obtient :
h100jzj100i=Z1
+1
(z)j100 (z)j2(dz)
=Z+1
1
zj100 (z)j2dz
Or 100 (z)est soit paire soit impaire ("parité dé…nie") sous inversion spatiale (c’est-à-dire, pour nous, quand
zdevient z), donc :
100 (z) = 100 (z)ou 100 (z)
d’où :
j100 (z)j=j100 (z)jdans les 2 cas
et …nalement :
h100jzj100i=Z+1
1
zj100 (z)j2dz
=h100jzj100i
= 0
Il n’y a pas d’e¤et Stark du 1er ordre pour le niveau fondamental de l’atome d’hydrogène (sans spin).
A.3 Donner l’expression de la correction au 2nd ordre 2E1du niveau fondamental (en faisant apparaître
le facteur (eE)2=EI). De quel signe est-elle ?
2E1=X
n>1X
l;m
jh100jWjnlmij2
E1En
: somme sur tous les états propres autres que j100i
E1En=EI11
n2<0 =)2E1<0
2E1= (eE)2
EI!0
@X
n6=1 X l;m
jh100jbzjnlmij2
11
n21
A<0
A.4 On peut montrer que les éléments de matrice hnlmjWjn0l0m0isont nuls lorsque l+l0est pair (pour
des questions de parité) ou lorsque m6=m0(car Lzcommute avec W). Donner les 3 premiers termes de
l’expression de 2E1.
Il faut donc que :
m= 0 et limpair
dans la somme précédente pour que les termes h100jbzjnlmisoient non nuls, d’où :
2E1= (eE)2
EI!0
@X
n>1X
limpair
jh100jbzjnl0ij2
11
n21
A
3

n= 2 =)l= 0 ou 1, mais seul l= 1 (impair) convient
=)terme : jh100jbzj210ij2
3=4
n= 3 =)l= 0;1ou 2, mais seul l= 1 (impair) convient
=)terme : jh100jbzj310ij2
8=9
n= 4 =)l= 0;1;2ou 3, mais seuls l= 1 et l= 3 (impairs) conviennent
=)termes : jh100jbzj410ij2+jh100jbzj430ij2
15=16
donc :
2E1= (eE)2
EI!4 3jh100jbzj210ij2+9 8jh100jbzj310ij2
+16
15 jh100jbzj410ij2+jh100jbzj430ij2+:::
A.5 La somme des di¤érents termes de l’expression de 2E1conduit au résultat suivant :
2E1=1
2E2avec : = 18"0a3
0(polarisabilité)
où "0= 8;85:1012Kg1m3A2s4est la permittivité du vide et où a0= 5;3:1011mest le rayon de Bohr.
Quelle est la valeur de 2E1(en eV ) pour un champ électrique de 104V=cm ? Comparer cette valeur à l’écart
entre les niveaux E1et E2. Conclusion.
2E1=1
2E2'3:1029J'2:1010eV
jE1E2j=EI11
4=3 4EI'10eV
2E1<< jE1E2j
=)calcul de perturbation justi…é !
B - Perturbation du niveau n= 2 et levée de dégénérescence
B.1 Quelle est la dégénérescence du niveau n= 2 ? Quels sont les états associés ?
n= 2 =)n2= 4 :E2dégé 4fois
n= 2 =)l= 0 (et donc m= 0) ou l= 1 (et donc m=1;0ou 1)
Etats associés : j200i;j210i;j211i;j21 1i
4

B.2 Sachant que seuls les 2éléments de matrice suivant sont non-nuls :
h200jWj210i=h210jWj200i= 3a0eE
déterminer les corrections du 1er ordre à l’énergie E2.
La matrice de Wdans le sous-espace sous-tendu par fj200i;j210i;j211i;j21 1ig (vecteurs de base pris
dans cet ordre) s’écrit :
W= 3a0eE 0
B
B
@
0100
1000
0000
0000
1
C
C
A
*j211iet j21 1isont donc VP de Wpour la vp 0(ie que Wn’a aucun e¤et sur ces vecteurs).
* Il ne reste donc qu’à diagonaliser la sous-matrice :
3a0eE 0 1
1 0 
3a0eE
3a0eE = 0
ie :
=3a0eE
donc :
E2= 0 ou 3a0eE
B.3 En combien de niveaux di¤érents se scinde le niveau n= 2 sous l’e¤et de W?
Le niveau E(0)
2se scinde donc en 3 niveaux :
(E2)1=E(0)
23a0eE
(E2)2=E(0)
2+ 3a0eE
(E2)3= (E2)4=E(0)
2(dégénérée 2 fois)
Il n’y a que levée partielle de dégénérescence.
B.4 Quels sont les nouveaux états propres ?
Les nouveaux états propres associés aux valeurs propres 3a0eE sont solutions de :
3a0eE 0 1
1 0   =3a0eE 
ie :
(j200ij210i)=p2
Les (nouveaux) états propres associés (base dite "adaptée") sont donc :
j'2i1= (j200i+j210i)=p2
j'2i2= (j200ij210i)=p2
j'2i3=j211i
j'2i4=j21 1i
5