Maths - Page d`accueil

II) EXPLOITER LES SYMÉTRIES D’UNE FONCTION POUR RÉDUIRE LE DOMAINE D’ÉTUDE
PROGRAMME DE KHÔLLE DE LA SEMAINE N°4
Une planche d’oral doit comporter une question de cours et deux (ou trois) exercices.
La question de cours peut porter sur une définition ou un résultat dont l’élève doit pouvoir donner un énoncé précis
qu’il doit pouvoir l’illustrer d’exemples, de contre-exemples, de schémas,etc...
Il pourra aussi répondre à des questions permettant à l’enseignant de s’assurer de la compréhension de la notion.
La question de cours peut aussi être un exercice simple d’application du cours ou l’exposé d’une méthode classique.
Elle pourra parfois consister à énoncer et à démontrer un théorème (cf. liste des démos exigibles)
La question de cours ne doit pas dépasser 20 mn et pourra ne pas être terminée si l’élève ne connaît pas son cours.
Un cours non su entraînera systématiquement une note inférieure à 10! (voire une exclusion de khôlle)
Le premier exercice sera un exercice d’application proche des exercices traités en classe. Il doit évaluer l’acquisition
de technique élémentaire du cours et les compétences calculatoires de bases des élèves.
Les exercices suivants sont libres dans la limite du cadre du programme de la semaine de khôlle.
N’oubliez pas de rendre votre compte-rendu de khôlle avant la fin de la semaine 5.
•Cours :CHAPITRE I TECHNIQUES FONDAMENTALES DE CALCUL EN ANALYSE
ÉTUDIER UNE FONCTION
I) Définir une fonction
Les élèves doivent :
• connaître et maîtriser le langage usuel des applications numériques (variable, expression, ensemble de définition,
domaine de valeurs, image et antécédent d’un réel, image directe et réciproque d’une application, restriction,
prolongement, représentation graphique)
• préciser les notions précédente sur des cas concrets simples graphiquement et/ou analytiquement
• déduire de graphe d’une fonction fcelui d’autres fonctions obtenues par des transformations géométriques
simples (translation, symétrie, élongation verticale ou horizontale)
PROPRIÉTÉS DES FONCTIONS DE RÉFÉRENCE (FICHE BILAN)
2ND DEGRÉ,EXPONENTIELLE,LOGARITHME,VALEUR ABSOLUE ET PARTIE ENTIÈRE
• connaître et utiliser les propriétés des fonctions polynômiales du second degré (racine, signe, factorisation, somme
et produit des racines)
• connaître et utiliser les propriétés des fonctions exponentielle et logarithme
• connaître et utiliser les propriétés de la valeur absolue
• résoudre des équations ou inéquations faisant intervenir ces fonctions usuelles en étant attentif aux connexions
logiques (implication, équivalence)
• connaître et utiliser le résultat dit de croissance comparée et les limites indéterminées levées par taux d’accrois-
sement.
II) Exploiter les symétries d’une fonction pour réduire le domaine d’étude
Les élèves doivent :
• connaître et maîtriser les notions de parité, imparité et périodicité et les conséquences graphiques
• utiliser les notions précédentes pour réduire un domaine d’étude dans le but d’étudier une fonction ou de ré-
soudre une équations ou inéquations.
PROPRIÉTÉS DES FONCTIONS DE RÉFÉRENCE (FICHE BILAN)
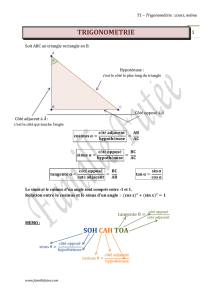
COSINUS,SINUS ET TANGENTE
• connaître et utiliser les propriétés des fonctions sinus, cosinus et tangente (la fonction cotan est hors programme)
• exploiter et utiliser le cercle trigonométrique pour trouver des lignes trigonométriques classiques et retrouver des
relations de trigonométrie élémentaires.
1/2

III) JUSTIFIER LA RÉGULARITÉ D’UNE FONCTION ET ÉTABLIR SON SENS DE VARIATION
• connaître et utiliser des relations de trigonométrie classique (angle double, formule d’addition et de factorisation,
transformation de Fresnel pour sinus et cosinus, angle double et tan(a+b) pour tangente)
• résoudre des équations du type cosa=cosb, sina=sinbet tan a=tanb
• résoudre des équations/inéquations trigonométriques en exploitant des relations de trigonométrie et/ou en fac-
torisant.
III) Justifier la régularité d’une fonction et établir son sens de variation
Les élèves doivent :
• pouvoir définir à l’aide de limite la notion de continuité, continuité à droite, à gauche et de prolongement par
continuité
• savoir justifier la continuité d’une application à l’aide des théorèmes usuels (en justifiant bien les hypothèses
pour le quotient et la composition)
• pouvoir utiliser le résultat sur la composition de fonctions monotones
• pouvoir définir à l’aide de limite la notion de dérivabilité, dérivabilité à droite, à gauche
• pouvoir lever des limites indéterminées qui s’interprètent comme des taux d’accroissement
• savoir justifier la dérivabilité d’une application à l’aide des théorèmes usuels (en justifiant bien les hypothèses
pour le quotient et la composition)
• mener une étude ponctuelle pour la dérivabilité aux points de continuité non pris en charge par les théorèmes
usuels
• savoir calculer le nombre dérivée, étudier son signe et dresser un tableau de variation
• connaître la régularité et le calcul de la dérivée pour les fonctions usuelles rencontrées (voir fiche bilan) en appli-
quant éventuellement les règles usuels (combinaison linéaire, produit, quotient, composition)
• avoir l’initiative d’introduire et d’étudier une fonction pour établir une inégalité
PROPRIÉTÉS DES FONCTIONS DE RÉFÉRENCE (FICHE BILAN)
COSINUS ET SINUS HYPERBOLIQUE
• connaître et utiliser les propriétés des fonctions ch et sh (la fonction th est hors programme)
Les seules relations de trigonométrie hyperbolique exigibles sont celles du cours. Tout autre relation devra être démontrée.
• résoudre des équations ou inéquations faisant intervenir ces fonctions (et anticiper éventuellement l’allure de
l’ensemble des solutions à l’aide de la représentation graphique)
• calculer pratiquement (dans l’optique de la physique et de la SI) des dérivées partielles premières et secondes
(pas de problème d’existence) en maîtrisant les notations ∂f
∂x,∂2f ∂x∂y
Attention! Les parties IV, V et VI n’ont pas été traitées
Pas de méthode pour justifier la non-existence d’une limite.
Pas d’étude asymptotique
•Exercices :(Listes des exercices traités en classes)
Exemples 1 à 11 , Exercice A-1 à A-5, Exercice R-1 et R-3
Une proposition de rédaction (voir TD) a été proposée pour les exercices : A-1, A-2, A-3, A-4 (A, C et D) et R-3.
•démos :(Listes des démonstrations exigibles)
Pas de démonstration exigible cette semaine
FIN
2/2