devoir surveille de physique n°1

PC*1 / PC*2 / PC 2014 / 2015 Devoir surveillé n°1 6 / 9 /14
1
PC*1 / PC*2 / PC DEVOIR SURVEILLE DE PHYSIQUE N°1
6 septembre 2014
PROBLEME 1 : ASSOCIATION DE CIRCUITS RC
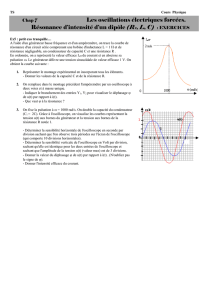
On analyse, à l'aide d'un oscilloscope, le circuit ci-contre comportant
un générateur de tension
E ,r
( )
, représenté dans le cadre pointillé,
en série avec une résistance connue R, un condensateur C et un
interrupteur K.
L'interrupteur est fermé à t = 0 alors que le condensateur est déchargé.
Les voies A et B de l'oscilloscope sont reliées aux deux bornes de la
résistance R. On note
u( t )
la tension aux bornes du condensateur
et
i( t )
l’intensité circulant dans le circuit.
L'enregistrement des signaux de l'oscilloscope donne l'oscillogramme suivant, avec les sensibilités 1 V/carreau
en vertical et 0,1 ms/carreau en horizontal. Les deux curseurs (lignes horizontales en pointillés) sont réglés pour
correspondre respectivement à 10 % et 90 % de l'amplitude maximale du signal (1).
I Réponse indicielle d’un circuit RC
1) Identifier, en le justifiant, les enregistrements (1) et (2) aux voies A et B
2) Etablir les lois de
u( t )
, tension aux bornes du condensateur, et
i( t )
courant dans le circuit.
On précisera la constante de temps τ et on déterminera l'expression de
t1
pour lequel :
u( t1)=0,9E
.
3) Préciser l’expression de la tension au point P. Sachant que R =100 Ω, déterminer les caractéristiques
E ,r
( )
du générateur de tension, puis en déduire la valeur de la capacité C.
4) On veut appliquer un échelon de tension au dipôle RC : sur quel paramètre du montage doit-on agir, et
comment ?
Le signal de sortie s’appelle alors réponse indicielle. Pourquoi peut-on dire que l’étude de la réponse
indicielle renseigne sur la “réactivité “ d’un circuit ?
R
C
r
voie B
E
K
voie A
P
(1)
(2)
•

PC*1 / PC*2 / PC 2014 / 2015 Devoir surveillé n°1 6 / 9 /14
2
II Réponse harmonique d’un circuit RC
On considère maintenant le circuit RC soumis à une excitation sinusoïdale
e( t ) =E cos( !t )
5) Déterminer la fonction de transfert
H1( j!)
en sortie ouverte (rien
n’est relié à la sortie) de ce circuit, et préciser l’expression de la pulsation
de coupure à –3 dB, que l’on notera
!0
.
6) En épreuve de travaux pratiques, on demande de fabriquer un filtre de fréquence de coupure (à –3 dB)
f0
= 5 kHz, et de gain (en dB) nul dans la bande passante.
La tension de sortie est observée sur un oscilloscope dont l’entrée peut être modélisée par l’association
en parallèle d’une résistance
Re
= 1 MΩ et d’un condensateur de capacité
Ce
= 30 pF
On dispose pour fabriquer ce filtre de deux résistances, respectivement de 4,7 kΩ et 680 kΩ, et de deux
condensateurs de capacité 6,8 nF et 47 pF.
Choisir les composants permettant de réaliser ce filtre et d’observer au mieux à l’oscilloscope le signal
de sortie. Une réponse argumentée et quantifiée est attendue. On pourra en particulier comparer les
valeurs du gain en bande passante et de la fréquence de coupure avec ou sans l’oscilloscope branché.
III Deux circuits RC en cascade
7) On associe maintenant deux modules RC en cascade.
Déterminer la fonction de transfert
H2( j!)
en sortie ouverte
de ce circuit, et préciser l’expression de
!2
, la pulsation de
coupure à –3 dB, en fonction de
!0
.
8) Montrer que
H2( j!)
peut se mettre sous la forme
H2( j!)=H0
1+j!
!"
#
$
%&
'
(1+j!
!)
#
$
%&
'
(
,
et exprimer
!"
et
!"
en fonction de
!0
9) Les deux modules RC sont maintenant associés par
l’intermédiaire d’un amplificateur opérationnel (AO) idéal.
fonctionnant en régime linéaire.
On précise que dans ce cas, les potentiels aux bornes
d’entrée + (non inverseuse) et – (inverseuse) sont égaux, et
qu’aucun courant ne rentre dans l’AO par les bornes + et –
a) Justifier l’appellation de suiveur donné à l’AO dans ce montage.
b) Déterminer la fonction de transfert en sortie ouverte de ce circuit, et préciser l’expression de ,
la pulsation de coupure à –3 dB, en fonction de .
c) Quel est l’intérêt d’utiliser des AO en suiveur dans les associations de cellules RC ?
10) Représenter sur un même graphe les diagrammes de Bode en amplitude associés aux fonctions de
transfert
H2
et
H3
. Commenter.
11) Proposer un montage pour fabriquer un filtre passe bas présentant une atténuation de 80 dB / décade
pour des pulsations grandes devant
!0
.
H3( j!)
!3
!0
s
R
e
C
R
e
C
s
R
C
s
AO
R
-
+
C
R
e
C
B
A

PC*1 / PC*2 / PC 2014 / 2015 Devoir surveillé n°1 6 / 9 /14
3
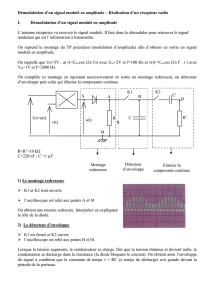
PROBLEME 2 : MODELISATION ET ANALYSE D’UN FILTRAGE
Un quadripôle est constitué de deux dipôles
D
1
et
D2
, disposés comme
l’indique la figure.
Seules les bornes d’entrée et de sortie sont accessibles à
l’expérimentateur. Ce dernier alimente le filtre par un générateur de tension
sinusoïdale parfait
e( t ) =E0cos!t
, et effectue une étude en fréquence de la
réponse du système.
Il relève le tracé expérimental suivant qui a été modélisé avec un tableur à l’aide de la fonction de transfert
H( j!)=1
1+jQ !
!0
"!0
!
#
$
%&
'
(
1) Déterminer les valeurs numériques de
0
ω
et Q.
2) Effet du filtre sur un signal non sinusoïdal.
On peut décomposer les signaux périodiques de période
T=2!
"
, d’entrée et de sortie sous la forme :
e( t ) =En
n=0
!
"cos( n#t+$n)
et
s( t ) =Sn
n=0
!
"cos( n#t+$n)
.
On définit le taux de distorsion harmonique par
!=
Sn
2
n=2
"
#
S1
.
a) Relier
n
S
à
n
E
grâce à la fonction de transfert.
b) On applique un signal périodique avec T =1 ms et
E0=
1 V de la forme suivante :
D1
D2
1,16 kHz
f
G
dB
- 3
0
0,34 kHz
t
La décomposition de Fourier de ce signal est
donnée par l’expression :
avec .

PC*1 / PC*2 / PC 2014 / 2015 Devoir surveillé n°1 6 / 9 /14
4
Montrer que le signal de sortie pour T =1 ms et
E0=
1 V est, en bonne approximation, sinusoïdal.
c) On s’intéresse maintenant au signal suivant, toujours de période T =1 ms, et avec et
E0=
1 V:
Peut-on encore considérer le signal de sortie comme sinusoïdal ?
3) Résolution de problème : détermination des composants du filtre.
On sait que le constructeur a utilisé pour construire le filtre un seul résistor de résistance R, un seul
condensateur de capacité C et une seule bobine d’inductance L. Ces trois dipôles ont été associés en série
ou en parallèle de façon à former les dipôles
D
1
et
D2
. Pour avoir des informations supplémentaires sur le
filtre, l’expérimentateur relie l’entrée du filtre à un générateur de tension continu de f.e.m
U0
= 15 V, la
sortie étant ouverte. Il mesure alors en régime établi un courant d’entrée d’intensité
I0
= 15 mA.
a) Déterminer la disposition des composants dans le quadripôle.
b) Déterminer la valeur numérique des composants.
PROBLEME 3 : ETUDE D’UN DISPOSITIF TMD (TUNED MASS DAMPER)
Exploiter le document joint en annexe pour répondre aux questions suivantes. On modélisera une construction
par un système masse-ressort subissant un amortissement.
1) En exprimant la fréquence d’oscillation du système, justifier qualitativement la relation donnée dans le
document entre la taille des bâtiments et leur fréquence d’oscillation.
2) Donner l’expression de l’amplitude de vibration du système relaxant au cours du temps. Justifier alors
quantitativement l’affirmation relative à la tour Citicorp : «…avec une période de 6,5 s et une diminution
d’amplitude de 1% par cycle, il faut une bonne dizaine de minutes pour que la vibration s’éteigne d’elle
même ».
3) Tracer l’allure de la courbe de la réponse du système à une excitation sinusoïdale. Vérifier que :
«… lorsque les vibrations de la tour sont rapides, la masse tend à rester immobile par rapport au sol. » en
donnant un sens physique explicite à l’expression « vibrations rapides ».
4) Le document dit que « La tour Taipei 101 oscille avec une période de 6,8 s et une amplitude maximale de
quelques dizaines de centimètres ». Calculer la valeur numérique de l’amplitude de son accélération et
vérifier qu’elle est de l’ordre « de quelques centièmes de l’accélération de la pesanteur ». Comparer ces
valeurs avec celle d’un bateau pour vérifier que l’oscillation de cette tour peut « donner la nausée. »
5) A quel type d’oscillateur est comparé le dispositif avec la boule d’acier installé pour limité les oscillations
de la tour Tapei 101 ? Vérifier que la fréquence propre de cet oscillateur est comparable à celles des
grattes ciels données par le document.
t en ms
La décomposition de Fourier de ce signal est
cette fois-ci donnée par :

PC*1 / PC*2 / PC 2014 / 2015 Devoir surveillé n°1 6 / 9 /14
5
PC*1 / PC*2 / PC CORRECTION DU DEVOIR SURVEILLE DE PHYSIQUE N°1
6 septembre 2014
PROBLEME 1 : ASSOCIATION DE CIRCUITS RC
I Réponse indicielle d’un circuit RC
1) La tension aux bornes d’un condensateur est continue. La courbe (1), image de
u( t )
est relevée sur la voie B.
La courbe (2) est l’image de la tension aux bornes du générateur.
2) On a l’équation de maille
E=R+r
( )
i( t ) +u( t )
avec
i( t ) =Cdu
dt
soit
du
dt
+u
!
=E
!
avec
!=R+r
( )
C
de solution générale
u( t ) =Aexp !t
"
#
$
%&
'
(+E
Par continuité de
u( t )
,
0=A+E
ce qui conduit à
u( t ) =E1!exp !t
"
#
$
%&
'
(
#
$
%&
'
(
On déduit
i( t ) =Cdu
dt
soit
i( t ) =CE
!exp "t !
#
$
%&
'
(=E
R+rexp "t !
#
$
%&
'
(
On a
u( t1)=E1!exp !t1
"
#
$
%&
'
(
#
$
%&
'
(=0,9E
soit
exp !t1
"
#
$
%&
'
(=0,1
et
t1=Ln10
( )
!
t1=2,3!
3) Le point P correspond à la tension
e( t ) =E!ri( t )
aux bornes du générateur à l’instant
t=0+
:
soit
e( t ) =E1!r
R+rexp!t "
#
$
%&
'
(
et
e( 0+)=R
R+rE
Pour
t! "
,
u!E
: on lit 6 carreaux soit 6 V E = 6 V
Le point P est situé à 4 carreaux :
R
R+r
E=4V
. Avec R = 100 Ω, on trouve r = 50 Ω
L’intersection de la courbe (1) avec le niveau 90% a lieu à
t1
= 4 × 0,1 = 0,4 ms
On en déduit
!=t1
2,3
=
0,17 ms puis
C=!
R+r
soit C = 1,1 µF
4) Un échelon de tension est un signal du type
e( t ) =0
pour
t
< 0, et
e( t ) =E
pour
t
≥ 0. Il faut idéalement un
générateur de résistance interne nulle, ou en pratique, négligeable devant R.
La réponse indicielle donne accès à la constante de temps
!=RC
du circuit seul, qui est un ordre de grandeur
du temps nécessaire à l’établissement du régime permanent.
II Réponse harmonique d’un circuit RC
5) Question de cours : on est en présence d’un pont diviseur, on a immédiatement
H1( j!)=S
E
=ZC
ZC+R
=
1
jC!
1
jC!
+R
=1
1+jRC!
. On reconnaît un passe bas d’ordre 1 de la forme
H1( j!)== 1
1+j!
!0
de pulsation de coupure ( à –3 dB)
!0=1
RC
6) Avec
f0=
!0
2"
=1
2"RC
= 5.103 Hz , on trouve RC = 32 µs