1 Variables aléatoires à densité 2 Loi uniforme

1 Variables aléatoires à densité
Le contenu de ce premier paragraphe ne fait pas partie des exigibles du programme de Mathématiques de
Terminale STL.
Son exposé a pour unique but de faciliter la compréhension des paragraphes suivants.
Définition
Soit Ωl’univers (i.e. l’ensemble des issues) d’une expérience aléatoire.
Une variable aléatoire Xdéfinie sur Ωest dite continue lorsqu’elle peut prendre comme valeur tous les
réels d’un intervalle Ide R, non vide et non réduit à un point.
Définition
Une fonction fdéfinie sur Rest appelée fonction de densité ou, par abus de langage, densité, si :
•fest continue et à valeurs positives sur R;
•l’aire de la partie du plan délimitée par la courbe représentative de fet par l’axe des abscisses est égale
à une unité d’aire.
Définition
Soit Ωl’univers d’une expérience aléatoire et Xune variable aléatoire continue, définie sur Ωet de densité f.
On appelle probabilité de l’événement (X∈I), où Iest un intervalle de R, et on note P(X∈I), l’aire
du domaine suivant :
{M(x;y); x∈Iet 06y6f(x)}
Propositions
Soient aet bdeux réels tels que a < b et Xune variable aléatoire continue, de densité f.
•La probabilité que Xprenne la valeur aest nulle (i.e. P(X=a) = 0).
•P(X < a) = P(X6a)et P(X > a) = P(X>a)
•P(X∈[a;b]) = P(X∈]a;b]) = P(X∈[a;b[) = P(X∈]a;b[)
2 Loi uniforme
Définition
Soient aet bdeux réels tels que a < b.
Une variable aléatoire Xsuit la loi uniforme sur l’intervalle [a;b]lorsque, pour tout intervalle Iinclus dans
[a;b], la probabilité de l’événement (X∈I)est égale à l’aire du domaine {M(x;y); x∈Iet 06y6f(x)}
où fest la fonction constante définie sur [a;b]par f(x) = 1
b−a.
Dans ces conditions, la fonction fest appelée fonction de densité de la loi uniforme sur [a;b].
1
b−a
ab
• •
I
[ ]
C
f
P(X∈I)
Proposition
Soient a,b,cet dquatre réels tels que a6c < d 6b.
Si une variable aléatoire Xsuit la loi uniforme sur [a;b]alors P(c6X6d) = d−c
b−a.
Définition
Soient aet bdeux réels tels que a < b et Xune variable aléatoire à densité sur [a;b]de fonction de
densité f.
On appelle espérance de Xle réel E(X)défini par E(X)=Zb
a
x×f(x) dx.

Proposition
Si une variable aléatoire Xsuit la loi uniforme sur [a;b]alors E(X) = a+b
2.
Définitions
Soient aet bdeux réels tels que a < b et Xune variable aléatoire à densité sur [a;b]de fonction de
densité f. On appelle :
•variance de Xle réel V(X)défini par V(X)=Zb
a
(x−E(X))2×f(x) dx;
•écart-type de Xle réel σ(X)défini par σ(X) = »V(X).
Proposition
Si une variable aléatoire Xsuit la loi uniforme sur [a;b]alors V(X) = (b−a)2
12 et σ(X) = b−a
√12 .
3 Loi exponentielle
Définition
Soit λun réel strictement positif.
Une variable aléatoire X, à valeurs dans [0; +∞[, suit la loi exponentielle de paramètre λlorsque, pour
tout intervalle borné Iinclus dans [0; +∞[, la probabilité de l’événement (X∈I)est égale à l’aire du
domaine {M(x;y); x∈Iet 06y6f(x)}où fest la fonction définie sur [0; +∞[par f(x) = λe−λx.
Dans ces conditions, la fonction fest appelée fonction de densité de la loi exponentielle de paramètre λ.
I
[ ]
C
f
P(X∈I)
Propositions
Soient cet ddeux réels tels que 06c < d.
Si une variable aléatoire Xsuit la loi exponentielle de paramètre λalors :
•P(c6X6d) = e−λc −e−λd ;•P(X6d) = 1 −e−λd.
Définition
Soient λun réel strictement positif et Xune variable aléatoire qui suit la loi exponentielle de paramètre λ.
On appelle espérance de X, et on note E(X), le réel défini par E(X) = lim
t→+∞Zt
0
x×f(x) dx, où fest la
fonction de densité de la loi exponentielle de paramètre λ.
Proposition
Si une variable aléatoire Xsuit la loi exponentielle de paramètre λalors E(X) = 1
λ.

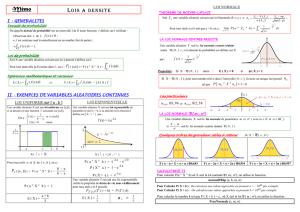
4 Loi normale
Définition
Soient µun réel et σun réel strictement positif.
Une variable aléatoire Xsuit la loi normale N(µ;σ)lorsque, pour tous réels aet btels que a < b :
P(a6X6b) = Zb
a
f(x) dxavec f:x7→ 1
σ√2πe
−
1
2Åx−µ σã2
Dans ces conditions, la fonction fest appelée fonction de densité de la loi normale de paramètres µet σ.
Remarque :
En pratique, on n’utilisera jamais cette égalité pour calculer une probabilité car on ne connaît pas de
primitive de la fonction f.
Dans le cadre de la loi normale, le calcul de probabilités est effectué à l’aide de la calculatrice.
Proposition
Si une variable aléatoire Xsuit la loi normale N(µ;σ)alors E(X) = µet σ(X) = σ.
Quelques informations sur la fonction de densité de la loi normale N(µ;σ)
Soient µun réel et σun réel strictement positif, f:x7→ 1
σ√2πe
−
1
2Åx−µ σã2
et C
fsa représentation
graphique dans un repère orthogonal du plan.
C
fest une courbe « en cloche », également appelée « gaus-
sienne », située au-dessus de l’axe des abscisses (fest à valeurs
strictement positives sur R).
Elle admet la droite d’équation x=µpour axe de symétrie (on
dit aussi qu’elle est « centrée en µ»).
Enfin, l’aire du domaine compris entre C
fet l’axe des abscisses
(« aire sous C
f») est égale à 1u.a.
Pour une même valeur de µ, plus σest grand, plus le sommet de
la courbe C
fest bas et plus la « cloche » est large.
C
f
x=µ
1
σ√2π
Aire égale
à1u.a.
C
f
x=µ
1
σ√2π
Méthode : Utilisation de la calculatrice graphique
Soient µun réel, σun réel strictement positif et Xune variable aléatoire suivant la loi normale N(µ;σ).
Obtenir le menu des distributions des lois de probabilités par : 2nd DISTR
•Pour calculer la probabilité P(a6X6b)où aet bsont deux réels connus tels que a < b :
normalFRép(a,b,µ,σ)
•Pour déterminer le réel atel que P(X6a) = poù pest un réel connu appartenant à ]0; 1[ :
FracNormale(p,µ,σ)
La calculatrice graphique ne permet pas le calcul direct de probabilités telles que P(X6a)ou P(X>a)
mais on peut aisément contourner ce problème.
⋆Si a6µalors :
•P(X6a)= P(X6µ)−P(a6X6µ)
= 0,5−P(a6X6µ)
•P(X>a)= P(a6X6µ) + P(X>µ)
=P(a6X6µ) + 0,5µa
X6a
µa
X>a
⋆Si a>µalors :
•P(X6a)= P(X6µ) + P(µ6X6a)
= 0,5 + P(µ6X6a)
•P(X>a)= P(X>µ)−P(µ6X6a)
= 0,5−P(µ6X6a)µ a
X6a
µ a
X>a

Proposition
Si une variable aléatoire Xsuit la loi normale N(µ;σ)alors :
P(X∈[µ−σ;µ+σ]) ≈0,683
µ
µ−σµ+σ
≈0,683 u.a.
P(X∈[µ−2σ;µ+2σ]) ≈0,954
µ
µ−2σ µ + 2σ
≈0,954 u.a.
P(X∈[µ−3σ;µ+ 3σ]) ≈0,997
µ
µ−3σ µ + 3σ
≈0,997 u.a.
Proposition
Si les conditions n>30,np >5et n(1−p)>5sont vérifiées, alors la loi B(n;p)admet pour approximation
la loi normale de même espérance et de même écart-type, c’est-à-dire la loi N(µ;σ)où µ=np et
σ=»np(1 −p).
Remarque :
Intuitivement, les trois conditions à remplir traduisent le fait que ndoit être suffisamment grand et pni
trop voisin de 0, ni trop voisin de 1.
Exemple :
Sur le graphique ci-dessous, on a représenté la probabilité P(X=k)en fonction de kquand Xsuit la loi
binomiale de paramètres n= 100 et p= 0,2.
On constate qu’il y a une certaine analogie entre la représentation graphique de la répartition des proba-
bilités de cette loi binomiale et la représentation graphique de la fonction de densité de la loi normale de
paramètres µ=np = 100 ×0,2 = 20 et σ=»np(1 −p) = √100 ×0,2×0,8 = 4.
k
p(X=k)
n= 100 et p= 0.2
C
foù f:x7→ 1
4√2πe
−
1
2Çx−20 4å2
0.05
0.10
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95100
Complément (hors programme) : La correction de continuité
Si une variable aléatoire Xsuit la loi B(n;p)et si les conditions n>30,np >5et n(1 −p)>5sont
vérifiées alors la loi de Xest « proche » de celle de la variable aléatoire Yqui suit la loi normale de même
espérance et de même écart-type, i.e. N(µ;σ)avec µ=np et σ=»np(1 −p).
Approcher une loi binomiale par une loi normale, c’est approcher une loi discrète (celle de X) par une loi
continue (celle de Y).
Or, pour une loi normale, comme pour toute loi continue, la probabilité d’une valeur isolée est nulle. Il
semble donc difficile de calculer P(X=k), pour un entier kcompris entre 0et n, avec cette approximation.
Afin de remédier à ce problème, on utilise la correction de continuité, qui consiste à remplacer la probabilité
de l’événement (X=k)par celle que Yappartienne à l’intervalle de longueur 1, centré en k.
On utilise alors les règles d’approximation suivantes :
•on approxime P(X=k)par P(k−0,56Y6k+ 0,5) ;
•on approxime P(X6k)par P(Y6k+ 0,5) ;
•on approxime P(X < k)par P(Y6k−0,5) ;
•on approxime P(X>k)par P(Y>k−0,5) ;
•on approxime P(X > k)par P(Y>k+ 0,5).