Méthode de dichotomie

Méthode de dichotomie 1
Méthode de dichotomie
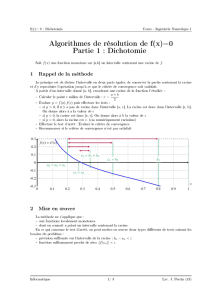
Étapes successives de la méthode de dichotomie avec comme point
de départ, l'intervalle [a1;b1]. Le zéro de la fonction est en rouge.
La méthode de dichotomie ou méthode de la
bissection est, en mathématiques, un algorithme de
recherche d'un zéro d'une fonction qui consiste à
répéter des partages d’un intervalle en deux parties puis
à sélectionner le sous-intervalle dans lequel existe un
zéro de la fonction.
Principe
On considère deux nombres a et b et une fonction f
continue sur l'intervalle [a, b] telle que f(a) et f(b)
soient de signes opposés. Supposons que nous voulions
résoudre l’équation f(x) = 0. Nous savons d'après le
théorème des valeurs intermédiaires que f doit avoir au
moins un zéro dans l’intervalle [a, b]. La méthode de
dichotomie consiste à diviser l’intervalle en deux en
calculant c = (a+b) / 2. Il y a maintenant deux
possibilités„: ou f(a) et f(c) sont de signes contraires, ou
f(c) et f(b) sont de signes contraires.
L’algorithme de dichotomie est alors appliqué au
sous-intervalle dans lequel le changement de signe se
produit, ce qui signifie que l’algorithme de dichotomie est en soi récursif.
L’erreur absolue de la méthode de dichotomie est au plus
après n étapes. En d’autres termes, l’erreur est diminuée de moitié à chaque étape, ainsi la méthode converge
linéairement, ce qui est très lent par comparaison avec la méthode de Newton.
L'avantage par rapport à cette dernière est son domaine d'application plus vaste : il suffit seulement que f(a) et f(b)
soient de signes opposés et qu'on puisse déterminer le signe de f(c) à chaque itération. De plus, si on se donne la
tolérance relative , on connaît en théorie le nombre maximum d'itérations nécessaires pour satisfaire cette
tolérance :
C'est un cas assez peu habituel en calcul numérique pour être noté.

Méthode de dichotomie 2
Programmation
Sous l'hypothèse que le signe de f(c) soit déterminable, voici une représentation de la méthode en langage Visual
Basic. Les variables xL et xR correspondent aux réels a et b précédents. Les valeurs initiales de xL et xR doivent
être choisies telles que f(xL) et f(xR) soient de signe opposé (elles encadrent le zéro). La variable epsilon
indique avec quelle précision le résultat doit être donné.
'Méthode de dichotomie
'Start loop
While (xR - xL) > epsilon do
'Calcule le milieu du domaine de définition
xM = (xR + xL) / 2
'Find f(xM)
If ((f(xL) * f(xM)) > 0) Then
'jette la moitié de gauche
xL = xM
Else
'jette la moitié de droite
xR = xM
End If
Loop
Limite de la méthode
Cette méthode d'une grande robustesse nécessite cependant de connaître à chaque étape le signe de f(c). Dans
quelques cas, il peut arriver que la valeur de f(c) soit si proche de 0 que la précision du logiciel de calcul ne permette
plus de déterminer le signe de f(c) (le logiciel de calcul assimile f(c) à 0). L'application de l'algorithme risque alors
de conduire à l'élimination erronée d'une moitié de l'intervalle et à la convergence vers une valeur éloignée de la
racine.
D'une manière plus générale, la détermination du signe de f(c) peut se révéler impossible, même en augmentant la
précision du calcul du logiciel. Considérons par exemple un réel dont on peut calculer des valeurs approchées
décimales ou rationnelles à toute précision désirée. Considérons maintenant la fonction f affine sur les
intervalles , et et telle que , , . La
méthode de dichotomie demande de déterminer le signe de . Or il n'existe aucun algorithme général
permettant de décider si , ou . En effet, un tel algorithme, s'il existait, ne devant effectuer
qu'un nombre fini de calcul, devrait prendre sa décision au vu d'un nombre fini de valeurs approchées , ce qui est
insuffisant pour conclure.
Cette limite conduit les théoriciens[1] de l'analyse constructive à qualifier la méthode de dichotomie de non
constructive et à privilégier l'énoncé alternatif : rechercher une valeur x telle que soit inférieure à une erreur
donnée.
Article détaillé : Analyse constructive.

Sources et contributeurs de l’article 4
Sources et contributeurs de l’article
Méthode de dichotomie „Source: http://fr.wikipedia.org/w/index.php?oldid=89927902 „Contributeurs: Achambily, Ambigraphe, Bdc43, Dake, Darkcrystal, Flo, Gédé, HB, Jct,
Jean-Charles.Gilbert, Khader hassen, Kilom691, Oxyde, Pixeltoo, Seb35, Theon, Zetud, 6 modifications anonymes
Source des images, licences et contributeurs
Image:Bisection_method.png „Source: http://fr.wikipedia.org/w/index.php?title=Fichier:Bisection_method.png „Licence: GNU Free Documentation License „Contributeurs: Berland, Dake,
Tokuchan, TommyBee, 3 modifications anonymes
Fichier:Nuvola apps kmplot.svg „Source: http://fr.wikipedia.org/w/index.php?title=Fichier:Nuvola_apps_kmplot.svg „Licence: GNU Lesser General Public License „Contributeurs:
Booyabazooka, Michael Reschke, Rocket000
Licence
Creative Commons Attribution-Share Alike 3.0
//creativecommons.org/licenses/by-sa/3.0/
1
/
4
100%