Un toboggan de plage (5,5 points) I. Mouvement de l`enfant entre D

Un toboggan de plage (5,5 points)
L'usage des calculatrices est autorisé.
Ce sujet ne nécessite pas de feuille de papier millimétré.
Un enfant glisse le long d'un toboggan de plage dans le référentiel terrestre supposé galiléen.
Pour l'exercice, l'enfant sera assimilé à un point matériel G et on négligera tout type de
frottement ainsi que toutes les actions dues à l'air.
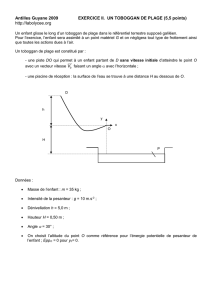
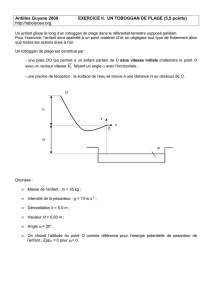
Un toboggan de plage est constitué par :
 une piste DO qui permet à un enfant partant de D sans vitesse initiale d'atteindre le
point O avec un vecteur vitesse faisant un angle α avec l'horizontale ;
 une piscine de réception : la surface de l'eau se trouve à une distance H au-dessous de
O.
Données :
Masse de l'enfant :
Intensité de la pesanteur :
Dénivellation :
Hauteur :
Angle : α = 30°
On choisit l'altitude du point O comme référence pour l'énergie potentielle de pesanteur de
l'enfant ; = 0 pour yo = 0.
I. Mouvement de l'enfant entre D et O
1. Donner l'expression de l'énergie potentielle de pesanteur de l'enfant au point D.
2. Donner l'expression de l'énergie mécanique de l'enfant au point D.
3. Donner l'expression de l'énergie mécanique de l'enfant au point O.
4. En déduire l'expression de la vitesse v0 en justifiant le raisonnement.
5. Calculer la valeur de la vitesse v0 de l'enfant en O.
6. En réalité, la vitesse en ce point est nettement inférieure et vaut
. Comment expliquez-vous cette différence ?

II. Étude de la chute de l'enfant dans l'eau
En O, origine du mouvement dans cette partie, on prendra
1. Énoncer la deuxième loi de Newton.
2. Appliquer la deuxième loi de Newton à l'enfant une fois qu'il a quitté le point O.
3. Déterminer l'expression des composantes ax(t) et ay(t) du vecteur accélération dans le
repère Oxy.
4. Déterminer l'expression des composantes vx(t) et vy(t) du vecteur vitesse dans le repère Oxy.
5. Déterminer l'expression des composantes x(t) et y(t) du vecteur position dans le repère Oxy.
6. Montrer que l'expression de la trajectoire de l'enfant notée y(x) a pour expression :
7. En déduire la valeur de l'abscisse xP du point d'impact P de l'enfant dans l'eau.
Corrigé
I. Mouvement de l'enfant entre D et O
1. L'altitude étant ici notée y, l'énergie potentielle de pesanteur est donnée par une relation de
la forme :
où E0 est une constante qui dépend de la référence choisie.
L'origine de l'axe (Oy) est choisi comme point de référence pour l'énergie potentielle de
pesanteur :
L'expression générale est donc
et, au point D,
2. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle de
pesanteur :
L'enfant part de D sans vitesse initiale, sa vitesse est alors nulle et son énergie cinétique
également.
Finalement,
3. Au point O c'est l'énergie potentielle de l'enfant qui est nulle (y = 0) ; sa vitesse vaut alors
.
On a donc
4. Puisque l'énoncé précise qu'on néglige les frottements et les actions de l'air, on applique
donc la conservation de l'énergie mécanique de l'enfant :
On en déduit
5. A.N. :
6. Cette différence traduit la dissipation d'un partie de l'énergie mécanique sous forme de
chaleur, en raison des frottements de l'enfant avec l'air et surtout avec le toboggan.
II. Étude de la chute de l'enfant dans l'eau

1. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées
au système est égale au produit de la masse m du système par l'accélération de son centre
d'inertie.
2. Une fois qu'il a quitté le point O, l'enfant n'est plus soumis qu'à son poids (on
néglige toujours les frottements de l'air) ; il est donc en chute libre.
En appliquant la deuxième loi de Newton au système enfant dans le référentiel terrestre
supposé galiléen, on obtient :
On en déduit :
3. Le vecteur champ de pesanteur est vertical, dirigé vers le bas.
Les coordonnées du vecteur accélération dans le repère (Oxy) sont donc :
4. Par définition, , donc et
Pour déterminer les coordonnées du vecteur vitesse, on intègre donc les expressions des
coordonnées du vecteur accélération :
où k1 et k2 sont des constantes.
Conditions initiales : à t = 0, l'enfant se trouve en O ; son vecteur vitesse a pour norme
et fait un angle avec l'horizontale.
Ses coordonnées sont donc
Finalement,

5. L'enfant est assimilé à un point matériel G, donc le vecteur position est noté .
Par définition, , donc et
Pour déterminer les coordonnées du vecteur position, on intègre donc les expressions des
coordonnées du vecteur vitesse :
où k3 et k4 sont des constantes.
Conditions initiales : à t = 0, l'enfant se trouve en O (0,0).
Ses coordonnées sont donc
Finalement,
6. Pour déterminer l'expression de la trajectoire, il faut exprimer t en fonction de x, puis
remplacer t par son expression dans .
donc
donc
7. L'ordonnée du point P est
est donc solution de l'équation du second degré :
soit
Il faut donc résoudre cette équation du second degré, de la forme
avec
Remarque : étant donnée la complexité des expressions, on privilégie une résolution
numérique de l'équation ; attention cependant à bien travailler en valeurs exactes du début à la
fin !
On calcule donc
Les solutions sont donc :
On élimine la deuxième solution car est positif.
La solution est donc