1. Définitions 2. Propriétés 3. Triangles égaux

1. Définitions
Définition :
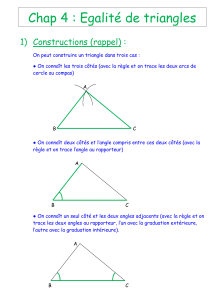
Une translation est une transformation qui permet de faire glisser une figure parallèlement à une droite sans
déformer ni retourner cette figure.
Définition :
Une rotation de centre et d’angle est une transformation qui permet de faire tourner une figure autour du
point d’un angle sans la déformer.
2. Propriétés
Propriétés :
Les translations et les rotations conservent les longueurs, l’alignement, les mesures d’angles et les aires.
Vocabulaire : Les transformations qui conservent les longueurs sont appelées des isométries. Les translations,
les rotations, les symétries axiales et les symétries centrales sont des isométries.
3. Triangles égaux
Définition :
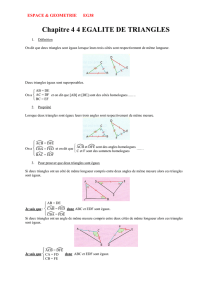
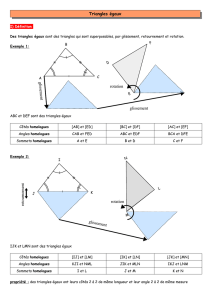
Des triangles égaux sont des triangles dont les côtés sont deux à deux de même longueur.
Remarque : Des triangles égaux sont superposables.
Propriété :
Si un triangle est l’image d’un autre triangle par une isométrie (translation, rotation, symétrie axiale ou
centrale), ou par une succession d’isométries, alors ils sont égaux.
Vocabulaire : Des triangles égaux sont aussi appelés triangles isométriques.
Propriété :
Si deux triangles sont égaux, alors ils ont des angles deux à deux de même mesure.
Propriété :
Si deux triangles ont un côté de même longueur et des angles adjacents à ce côté deux à deux de même mesure,
alors ces deux triangles sont égaux.
Exemple : Si
et ′ ′ ′ sont deux triangles tels que
=
et
=
et
=
, alors ils sont égaux.
Propriété :
Si deux triangles ont un angle de même mesure compris entre des côtés deux à deux de même longueur, alors
ces deux triangles sont égaux.
Exemple : Si
et ′ ′ ′ sont deux triangles tels que
=
et
=
et
= ′ ′, alors ils sont égaux.
Vocabulaire : Lorsque deux triangles sont égaux, deux côtés superposables sont dits côtés homologues, deux
angles superposables sont dits angles homologues, et les sommets correspondants sont dits sommets
homologues.