Chapitre n°6 : « Le parallélogramme »

5ème4 2009-2010
Chapitre n°6 : «
Chapitre n°6 : « Le parallélogramme Le parallélogramme » »
I. L'essentiel
Rappels
Un quadrilatère est une figure fermée constituée de quatre segments appelés côtés.
Vocabulaire
•
A
,
B
,
C
et
D
sont les sommets.
•
•
[AB ]
,
[BC ]
,
[CD ]
et
[DA ]
sont les côtés.
•Noms possibles :
ABCD
,
BADC
,
CDAB
…
•Côtés opposés :
[AD ]
et
[BC ]
;
[AB ]
et
[DC ]
•Côtés consécutifs :
[BA ]
et
[AD ]
;
[DC ]
et
[CB ]
…
•Diagonales :
[AC ]
et
[BD ]
.
•Angles opposés :
DAB
et
DCB
.
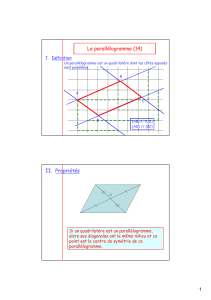
Définition
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Construction à la règle et à l'équerre
On a construit deux paires de droites parallèles :
•
d1// d2
•
d1'// d2'
Ces quatre droites forment quatre points :
A
,
B
,
C
et
D
.
ABCD
est un parallélogramme.
Construction à la règle et au compas
•On suppose les points
A
,
B
et
C
déjà placés.
On veut construire le point
D
tel que
ABCD
soit un parallélogramme.
•On prend l'écartement entre
A
et
B
et on
pointe sur
C
pour former un premier arc de
cercle.
•On prend l'écartement entre
B
et
C
et on
pointe sur
A
pour former un deuxième arc de cercle.
•On place le point
D
puis on trace le parallélogramme
ABCD
.

5ème4 2009-2010
Autre exemple
A
,
B
et
C
sont trois points quelconques. Construis le
point
D
tel que
BACD
soit un parallélogramme.
II. Propriétés
1/ Sur les côtés
Propriété
Dans un parallélogramme, les côtés opposés sont de même longueur.
Figure pour illustrer.
Les côtés opposés sont :
•
[IJ ]
et
[LK ]
•
[LI ]
et
[KJ ]
.
Donc
IJ =LK
et
IL=JK
.
2/ Sur les diagonales
Rappels
•
A
et
A '
sont symétriques par rapport à un point
O
si
O
est le milieu du segment
[AA' ]
.
•On rappelle aussi qu'un centre de symétrie est un point autour duquel la figure peut
effectuer un demi-tour puis revenir à sa place initiale (voir page 156)
Activité
Il semble que les longueurs
OB
et
OC
soient égales. De même pour les
DO
et
OA
.
Il semble donc que
O
soit le milieu des diagonales.
Définition
Le centre d'un parallélogramme est à l'intersection des diagonales

5ème4 2009-2010
Propriétés
•Les diagonales d'un parallélogramme se coupent en leur milieu.
•Le centre du parallélogramme est aussi le centre de symétrie.
Exemple
•Les parallélogrammes
sont :
ABFE
;
ADEC
.
•Dans
ABFE
les
longueurs égales sont :
AB=EF
AE=BF
AH =HF
EH =HB
•Dans
ADEC
les
longueurs égales sont :
DG =GC
AG=EG
AD=CE
DE =CA
3/ Sur les angles
Propriétés
Dans un parallélogramme, les angles opposés sont de même mesure.
Exemple
Dans le parallélogramme ci-
contre, on a :
•
CBA= CDA
•
BCD= BAD
(voir à la fin du chapitre pour l'autre propriété concernant les angles consécutifs)

5ème4 2009-2010
III. Constructions de parallélogramme (exemples)
Méthode générale
•On fait une figure à main levée la plus réaliste possible.
•On élabore une stratégie de construction.
•On fait la figure aux instruments.
Exemple 1
Construire un parallélogramme
ABCD
tel que
AD=4cm
et
DAB=60°
.
AB=5cm
•Figure à main levée :
•Je trace
AD=4cm
; je fais un angle à
60°
;
je trace
AB=5cm
. Pour construire le point
C
, j'utilise le compas.
Exemple 2
Construire le parallélogramme
IJKL
tel que
IJ =3,5 cm
;
JK =4,7 cm
et
IK =2,8 cm
•A main levée
•Avec les instruments
A
B
C
D4 cm
60° 5 cm
IJ
K
L
3,5 cm
4,7 cm
2,8 cm
(échelle 1/2)

5ème4 2009-2010
Exemple 3
Construire un parallélogramme
EFGH
tel que
FH =9cm
et
EG=5cm
.
FOG
=35°
•A main levée
•Aux instruments
IV. Propriétés réciproques
Propriété caractéristique n°1
Si un quadrilatère (non croisé) a ses côtés opposés de même longueur alors c'est un
parallélogramme.
Application
C'est la construction au compas vue au début du chapitre
On a construit le parallélogramme
ABCD
tel que
AB=CD
et
BC =AD
F
E
G
H
9 cm
5 cm
O
35°
(échelle 1/2)