3IMRT Circuit en régime sinusoidal forcé

3IMRT Circuit en régime sinusoidal forcé
Données : Pour une association série R-{L,r}-C soumise à une tension u(t) = UM.sin(.t + ) et traversée par un courant
d’intensité i(t) = I
M. sin(.t), on définit : Z =
2
2
totale C
1
LR   ; tan() =
totale
R
C
1
L
; cos() = Z
Rtotale
III –Résonance d’intensité d’un circuit RLC
On dispose des appareils suivants:
-un générateur de tension alternative sinusoïdale u = f(t) de valeur
efficace réglable de 0 à 10 V, de fréquence réglable de 5 à 5000 Hz ;
-un ampèremètre ;
-deux voltmètres ;
-une bobine d'inductance L et de résistance r ;
-un condensateur de capacité C ;
-une résistance R réglable de 0 à 1100 ;
-un oscillographe bicourbe.
1. En utilisant certains appareils cités ci-dessus, faire le schéma d'un montage simple qui permet d'étudier la variation de
l'intensité dans un circuit RLC série soumis à une tension sinusoïdale de fréquence variable.
Schéma comportant associés en série, le générateur, la résistance R, le condensateur, la bobine et
l’ampèremètre générateur iampèremètre
masse voie B voie A
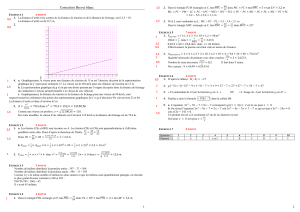
2. La mesure de l'intensité efficace dans le circuit en fonction de la fréquence permet de dresser le tableau suivant.
La tension efficace Ued'entrée est maintenue constante, égale à 5 V pour tout l'exercice.
2.1. Tracer la courbe I = f(N). Échelles : 1 cm représente 2,5 mA ; 1 cm représente 100Hz.
2.2. Que représente la fréquence N0correspondant au
maximum d'intensité ? Donner sa valeur.
N0est la fréquence de résonance d’intensité.
Intensité efficace maximale de valeur I0= 47,0 mA
pour N0= 700 Hz
2.3. Quelle est la résistance totale du circuit ?
A la résonance, l’impédance du circuit est égale à
sa résistance totale soit Z0= Rtotale = Ue/I0= 5/0,047
=106,4 
3.1. Représenter sur le schéma le branchement de
l'oscillographe bicourbe pour visualiser la tension u = f(t)
délivrée par le générateur sur la voie A et les variations
d'intensité sur la voie B.
3.2. Lorsque N = N0on observe l'oscillogramme numéro 1
(fig. 1) :
Figure 1 Figure 2

Déviation verticale voie A : 2 V.cm -1
Déviation verticale voie B : 1 V.cm -1
Balayage horizontal : 0,2 ms.cm -1
.
- Quelle courbe correspond à celle enregistrée sur la voie A?
Uemax = Ue
2
= 7,1 V donc dA= 7,1 V / 2 V.cm-1 = 3,5 cm: La courbe C1visualise la tension sur la voie A
- Quelle courbe correspond à celle enregistrée sur la voie B?
La courbe C2visualise alors la tension sur la voie B
- En déduire la valeur de la résistance R réglable puis celle de la résistance rde la bobine.
URmax = 2,5 cm x1 V.cm -1 = 2,5 V ; Les courbes sont en phase donc le circuit est à la résonance
et l’intensité efficace est I0; alors R = URmax / I0max = 2,5 / (0,047
2
) = 37,6 et r = Rtotale –R = 68,8
3.3. La tension efficace UCmesurée aux bornes du condensateur est alors maximale et vaut 21,5 V.
- Donner l'expression de la tension UCen fonction de R, r, C, No, Ue.
UC=0
0
I
C
avec I0=
e
U
R r
et  N0donc UC=e
0
U
2 (R r)CN
- En déduire la valeur de C : C = e
C 0
U
2 .(R r).U .N
  =5
2 106, 4 21, 5 700
   = 4,97 x 10-7 F≈500 nF
3.4. Calculer la valeur de l'inductance L : A la résonance LC
2= 1 donc L =
2
0
1
C
=
2 2
0
1
4 CN
= 0,103 H
4. On règle maintenant N de facon il obtenir l'oscillogramme de la figure 2.
4.1. Déterminer la fréquence N. : T = 8 cm x0,2 ms.cm-1 = 1, 6 ms ; N = 1/T = 1 / (1,6 x10-3) = 625 Hz
4.2. Déterminer la phase de i = g(t) par rapport à u = f(t) c’est-à-dire (i/u)
La courbe C1visualise la tension du générateur donc est la courbe d’amplitude constante, c’est-à-
dire celle qui a la même amplitude que la courbe C1de la figure 1 soit 3,5 cm. La courbe C2qui
visualise l’intensité apparaît alors décalée à gauche de 1 cm donc l’intensité est en avance sur la
tension u du générateur, soit (i/u) > 0.
(i/u) = 2t/T = 2x1/8 = /4 radian = 45 degrés
4.3. En prenant les valeurs de C, R et r trouvées précédemment, en déduire la valeur de l'inductance L
La comparer à celle trouvée à la question 4. (utiliser l’expression de tan( ) figurant dans les données)
i/u = -  u/i donc tan( i/u) = - tan( u/i) =
totale
1
L
C
R
alors L=
1
C
- Rtotale.tan(
i/u)
finalement : L=
2
1
C
- Rtotale.tan(
i/u) / ; L =
2 2
1
4 CN
- Rtotale.tan(
i/u) / 2N≈0,103 H
avec tan(
i/u) = tan(- 45°) = - 1 ; la valeur de L est confirmée