1. Masse volumique

1. Masse volumique
Définition:
La masse volumique ρ est définie comme étant la masse M par unité de volume V:
€
ρ =M
V
Unités:
€
kg
m3
ou éventuellement
€
g
cm3
.
Ordres de grandeur:
Matière
Eau
Air*
Aluminium
Fer
ρ
€
103kg
m3
€
≅1,3 kg
m3
*
€
2,7 ⋅103kg
m3
€
7,87 ⋅103kg
m3
* (dépend de la température et de la pression)
Calcul des volumes :
• Pour une sphère de rayon R,
€
V=4
3
π R3
• Pour un cylindre de rayon r et de hauteur h,
€
V= π r2h
.
Transformations d'unités:
Savoir convertir le litre et ses sous-multiples en m3.
Exemples: 1 ml = 1 cm3 = 10-6 m3 ; 1 l = 10-3 m3
Exercices :
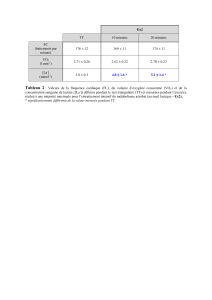
1. Calculer la masse volumique de la Terre et du Soleil (les rayons des astres et leur masse
se trouvent dans le Formulaire et Tables). Comparer et discuter les deux résultats.
Rép. 5,5 g/cm3 ; 1,42 g/cm3
2. Une bille en acier a un diamètre de 8 cm. Quelle est sa masse?
Rép. 2,10 kg
3. Un cylindre de hauteur 5 cm et dont le diamètre est de 3 cm, a une masse de 277 g. De
quelle matière est faite ce cylindre? Rép. 7,84 g/cm3 ; fer
4. On aimerait fabriquer une sphère en or dont la masse serait de 1 kg. Quel devrait être le
rayon de la sphère? Rép. 2,31 cm

2. Mouvement rectiligne uniforme (MRU)
Le MRU est un mouvement en ligne droite à vitesse constante v0 . Il est utilisé pour décrire le
mouvement et la trajectoire d'une voiture ou de tout autre véhicule se déplaçant en ligne
droite à une vitesse constante. Il s'applique en particulier aux sondes astronomiques qui ont
quitté le système solaire.
Définition :
La vitesse d'un mobile est définie comme le rapport entre la distance Δ x parcourue par le
mobile et le temps Δ t qu'il a fallu pour parcourir cette distance. Ainsi
€
v0=Δx
Δt
Unités :
€
v0
[ ]
=m/s
Loi du MRU:
Pour un MRU, la distance x parcourue durant le temps t par un mobile de vitesse v0 est :
€
x=v0⋅t + x0
Unités:
€
x
[ ]
=m
€
t
[ ]
=s
NB:
€
1 m
s=3,6 km h
x0 est la position de l'objet pour le temps t = 0. Si le problème ne comprend qu'un seul mobile,
on pourra toujours choisir x0 = 0.
Ordres de grandeur:
Vitesse de la lumière (notée c):
€
c=3⋅108 m/s
;Vitesse du son dans l'air :
€
vson =340 m/s
Vitesse d'un avion :
€
vavion =850 km/h
Exercices :
1. Quelle est la distance parcourue par la lumière en 1 an?
2. Un avion vole à 850 km/h. Combien de temps lui faut-il pour effectuer un vol de
1000 km? Pour effectuer un tour de Terre (rayon de la Terre : 6400 km) ?
3. Quelle est la vitesse d'un mobile qui parcourt 180 cm en 4 s?
4. Combien de temps faut-il à la lumière pour nous parvenir de la Lune? Du Soleil?
5. Un éclair tombe à 3 km de l'endroit où vous vous trouvez. Combien de temps faut-il au
son pour vous parvenir?
6. Quelle est la vitesse d'un point de l'équateur due à la rotation de la Terre sur elle-même?
7. Quelle est la vitesse d'un point situé à la latitude de Neuchâtel, vitesse due à la rotation
de la Terre sur elle-même?
8. Quelle est la vitesse de la Terre dans son mouvement autour du Soleil?
Ex1. 9,45.1015 m Ex2. 1 h 11 min ; 47 h 19 min ; Ex3. Rép. 0,450 m/s ;
Ex4. 1,28 s ; 8,33 min ; Ex5. Rép. 8,82 s ; Ex6. 465 m/s Ex7. 317 m/s Ex8. 29,9 km/s

3. Mouvement rectiligne uniformément accéléré (MRUA)
Un MRUA est un mouvement au cours duquel la vitesse change régulièrement et pour lequel
l'accélération est donc non-nulle. Il décrit le mouvement et la trajectoire d'objets qui tombent
grâce à la force d'attraction de la Terre, de véhicules qui freinent ou qui accélèrent, de mobiles
qui roulent le long de routes en pente, etc.
Définition :
Dans le cas d'un mouvement rectiligne, l'accélération d'un objet est définie comme le rapport
de la variation de la norme de la vitesse, Δ v et du temps Δ t qu'il a fallu pour que la vitesse
change de la quantité Δ v. Soit :
€
a=Δv
Δt
Unités [ a] = m/s/s = m/s2
Lois du MRUA :
La position d'un mobile au cours du temps pour un MRUA est donnée par :
€
x=1
2
a⋅t2 + v0⋅t + x0
où v0 est la vitesse du mobile au temps t=0 et x0 sa position au temps t=0.
La vitesse du mobile au cours du temps pour un MRUA est donnée par :
€
v=a⋅t + v0
Ordres de grandeur:
Accélération de la pesanteur : a=g=9,81 m/s2 ; voiture freinant sur route sèche : -5 à -7 m/s2
Exercices :
1. Une voiture passe de 0 à 100 km/h en 8,3 s. Quelle est son accélération? Quelle distance
la voiture parcourt-elle durant ce laps de temps? Rép. 3,35 m/s2 ; 115 m
2. Une voiture passe de 70 à 100 km/h en 7,8 s. Que vaut son accélération? Rép. 1,07 m/s2
3. Pour mesurer la profondeur d'un puits, on laisse tomber un caillou et on mesure le temps
de chute, t=1,44 s. Quelle est la profondeur du puits? Quel temps faut-il au son pour
nous parvenir? Rép. 10,17 m ; 30,6 ms
4. Un pot de fleur tombe depuis le 3ème étage du Lycée. Combien de temps dure la chute?
Quelle est la vitesse du pot juste avant de toucher le sol? Rép. 1,34 s ; 13,3 m/s
5. Un avion doit atteindre 500 km/h pour pouvoir décoller. Quelle doit être la longueur
minimale de la piste pour que les passagers ne soient pas soumis à une accélération
supérieure à g/5? Rép. 4,92 km
6. Les traces de freinage d'un voiture sont longues de 30 m . Le freinage a été brutal
puisque les passagers ont été soumis à une accélération de 10 m/s2 (1 g) . A quelle
vitesse roulait la voiture? Rép. 87,3 km/h

Energie, puissance, rendement
A. ENERGIE
Définition :
• L'énergie? On ne sait pas ce que c'est, mais ça se conserve... (R. Feynman)
• L'énergie? C'est du travail en boîte...
• L'énergie? C'est ce qui permet de produire de la chaleur, de la lumière, du travail, du
mouvement...
Une notion importante en physique est la notion de conservation: ne sont autorisés que les
phénomènes qui assurent la conservation l'énergie.
Unités : l'énergie se mesure en Joules [J]
La définition de l'énergie peut paraître difficile. Par contre, ce que l'on appréhende facilement,
ce sont les différentes formes que l'énergie peut prendre et qui peuvent se transformer l'une
dans l'autre : énergie cinétique, énergie potentielle, énergie thermique, énergie électrique, etc.
Nous donnerons ci-dessous une liste des différentes formes d'énergie avec des relations qui
permettent de calculer les quantités d'énergies mises en jeu.
B. PUISSANCE
Définition:
La puissance est l'énergie transférée par unité de temps
€
Puissance =Energie
Temps
ou
€
P=E
t
Unités: l'énergie est en Joules, le temps en seconde. La puissance est alors en Watt [W]
Notons que si la puissance est connue ainsi que le temps, on en tire que l'énergie vaut
€
E=P⋅t
C. RENDEMENT
Le rendement est défini comme le rapport de l'énergie utile sur l'énergie consommée.
€
η =Energie utile
Energie consommée =Euti Econs
que l'on peut aussi écrire comme
€
η =Puissance utile
Puissance consommée =P
uti
P
cons
Le rendement est toujours plus petit que 1 ou 100%.

4. Monter les escalier et... manger
Monter les escaliers demande un effort et exige donc de l'énergie. Celle-ci est prise dans les aliments que nous
mangeons : dans une telle situation, il y a transformation d'énergie chimique (prise dans les aliments) en énergie
potentielle de gravitation.
Energie potentielle de gravitation.
Monter des escaliers, gravir une montagne, hisser une charge demande de l'énergie, ces opérations ne s'effectuent
pas spontanément! L'énergie qu'il faut pour élever une charge d'une certaine hauteur dépend de la masse m de la
charge, de la hauteur
€
Δh
dont il faut l'élever et d'une constante g qui traduit le fait que nous sommes sur Terre et
non sur la Lune ou sur un autre astre. Pour la Terre,
€
g=9,81 N/kg
. L'énergie potentielle vaut :
Energie potentielle (de gravitation)
€
Epot =m⋅g⋅ Δh
[J] où
m est masse de la charge à élever en [kg]
€
Δh
est la hauteur en [m]
€
g=9,81 N/kg
Energie chimique.
Une voiture peut avancer grâce à son moteur qui est alimenté par de l'essence. Nos habitations sont chauffées au
bois, au gaz ou à l'aide d'autres combustibles que nous brûlons. Nous-mêmes sommes capables d'effectuer du
travail, de marcher, de monter les escaliers par le fait que nous consommons des aliments. Donc le bois, le gaz,
les produits pétroliers, le chocolat et les autres aliments contiennent de l'énergie qui est libérée par réaction
chimique avec l'oxygène. La quantité d'énergie chimique contenue dans un combustible dépend de la masse de
combustible et d'une grandeur caractérisant la réaction chimique de ce combustible. Ainsi:
Energie chimique
€
Echim =Mcomb ⋅PE
[J] où
€
Mcomb
est la masse de combustible en [kg]
€
PE
est la pouvoir énergétique du combustible en [J/kg]. Il se trouve dans les
Formulaires&Tables ou est indiqué sur les emballages des aliments
Exercices :
1. Que vaut l'énergie potentielle d'un objet de 100 g posé sur une surface à 1 m du sol? Rép. env. 1 J
2. Quelle quantité d'énergie faut-il fournir à un caillou de 150 g pour qu'il atteigne un hauteur de 25 m?
Rép. 36,8 J
3. Quelle est la quantité d'énergie chimique contenant dans 50 g de chocolat? 20 litres d'essence? Un m3 de
bois? Rép. env. 1 MJ ; 653 MJ ; 7200 MJ
4. Quelle quantité d'énergie faut-il pour monter une masse de 75 kg de 1000 m ? Rép. 736 kJ
5. Quelle quantité de chocolat un promeneur effectuant une ascension de 1000 m doit-il absorber pour
couvrir sa dépense d'énergie? Rép. 36,8 g
Si le promeneur effectue la montée en 3h30, quelle puissance développe-t-il ? Rép. 58,4 W
6. Dans les exercices 1 et 2 on n'a pas tenu compte du rendement musculaire. Or celui-ci est de l'ordre de
25%. Qu'est-ce que cela signifie et quelle incidence cela a-t-il sur les résultats précédents?
7. Un ascenseur a une masse de 500 kg et peut transporter 6 personnes de 80 kg chacune. Il est utilisé pour
monter de 5 étages (1 étage = 3 m). Quelle quantité d'énergie faut-il pour cela ? A quelle quantité de
produit pétrolier cela correspond-il? Rép. 144 kJ ; 3,21 g
8. Quelle doit être la puissance du moteur de l'ascenseur si la montée de 5 étages s'effectue en 18 s ?
Quelle est la vitesse moyenne de l'ascenseur? Rép. 8 kW ; 0,833 m/s