Exercice 1 – Vitesse de propagation des ondes dans une roche [5

SVT – Vendredi 18 mars 2016 – Devoir – Durée 55 minutes – Salle polyvalente – 1ere S3 – Calculatrice autorisée
Exercice 1 – Vitesse de propagation des ondes dans une roche [5 points]
Question : à partir d'informations tirées des documents qui suivent, indiquez la nature probable de la barre de roche
qu'un étudiant à trouver dans un placard du laboratoire de géologie en faisant du rangement.
Remarque : la réponse attendue à la question ne compte que pour 1 point. La démarche (présentation rigoureuse du raisonnement
et des calculs) compte pour 4 points.
Document A – Mesures faite sur la barre de la roche inconnue
Longueur de la barre de roche : 1,25 m.
Protocole :
On place sur cette barre deux capteurs piezo espacés de 1,15 m.
A l'aide du logiciel Audacity on enregistre les ondes produites par le choc d'un marteau à diapason sur une extrémité de la barre de
roche.
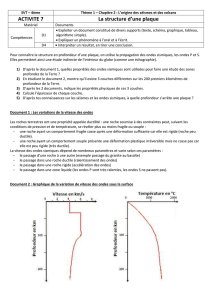
Document B : Copies d'écran de l'enregistrement des ondes, obtenu avec Audacity.
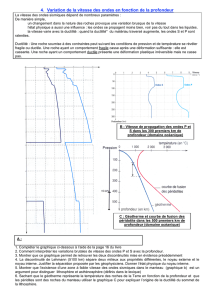
Document C : vitesse des ondes P dans diverses roches
Roche Calcaire Grès Granite Basalte Péridotite
Vitesse des ondes
P (km.s-1)6 6 6,25 6,75 ≥ 8

Pour déterminer la nature de la roche inconnue, nous allons comparer la vitesse de propagation d'ondes
dans cette roche à celle de roches connues (document C).
Pour déterminer la vitesse V de propagation d'ondes dans cette roche, on se base sur les mesures
effectuées et dont les résultats sont fournies dans les documents A et B.
Sachant que V (km.s-1) : D (km) ÷ T (s)
D : distance entre les deux capteurs piezo posés sur la barre de roche
D = 1,15 m
D = 1,15 × 10-3 km (puisque 1 m ≡ 10-3 km)
T : durée mise par les ondes pour parcourir la distance D
T1 : heure d'arrivée des ondes sur le premier capteur piezo.
T1 = 0,001716 s
T2 : heure d'arrivée des ondes sur le second capteur piezo
T2 = 0,001898 s
T = T2 – T1 T = 0,001898 – 0,001716 T = 0,000182 s T = 1,82 × 10-4 s
D'où :
V = 1,15 × 10-3 ÷ 1,82 × 10-4 V = 6,31868 km.s-1 V = 6,32 km.s-1
Or d'après le document C, la vitesse de propagation des ondes P la plus proche est celle d'un granite
(6,25 km.s-1).
Donc on peut supposer que cette roche inconnue est un granite.

Exercice 2 - Anomalies magnétiques de part et d’autre de la dorsale de Juan de Fuca [5 points]
Question : à partir des informations tirées du document qui suit, calculez la vitesse (en cm.an-1) d'expansion océanique
de part et d'autre de la dorsale de Juan de Fuca.
Remarque : le résultat attendu ne sera noté que sur 1 point. La démarche (présentation rigoureuse des calculs) pour y parvenir sera
notée sur 4 points.
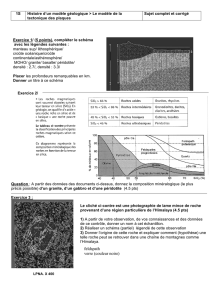
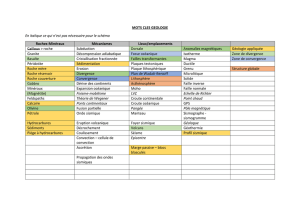
7,6 cm
4,5 cm

Pour déterminer la vitesse d'expansion de part et d'autre de la dorsale océanique de Juan de Fuca :
✗nous allons évaluer la distance (D) à laquelle est située aujourd'hui une des anomalies du champ
magnétique terrestre enregistré par le basalte de la croûte océanique, par rapport à l'axe de la
dorsale.
En effet nous savons que le basalte se forme au niveau de l'axe de la dorsale, à partir d'un magma
qui en refroidissant franchit la température de Curie, ce qui permet la « fossilisation » du champ
magnétique terrestre.
✗Ensuite nous chercherons l'âge (T) de l'anomalie du champ magnétique terrestre choisie, sachant
que cet âge correspond à la durée mise par le basalte pour parcourir la distance qui le sépare
actuellement de l'axe de la dorsale.
Nous allons nous baser sur le début de l'anomalie du champ magnétique terrestre d1.
Soit V la vitesse d'expansion (en cm.an-1) :
V = 2 × D (cm) ÷ T (an)
Soit D la distance qui sépare l'axe de la dorsale de Juan de Fuca du début de cette anomalie. On multiplie
cette distance par 2 puisque l'expansion se fait de chaque côté de l'axe de la dorsale
Document (mm) Réalité (km)
Échelle 47 120
Distance recherchée 28 D
D = (28 × 120) ÷ 47 D = 71,489 km D = 71,5 × 105 cm
Soit T l'âge du début de l'anomalie du champ magnétique terrestre d1 (en an).
Document (mm) Réalité (Ma)
Échelle 76 4
Age recherché 45 T
T = (4 × 45) ÷ 76 T = 2,368 Ma T = 2,37 × 106 an
V = (2 × 71,5 × 105) ÷ 2,37 × 106V = 6,0337 cm.an-1
D'après les données paléomagnétiques, la vitesse d'expansion du plancher océanique de part et d'autre de
la dorsale de Juan de Fuca est d'environ 6 cm.an-1.