Réactions acido-basiques I Autoprotolyse de l`eau Inévitablement a

Réactions acido-basiques - PCSI 1/5
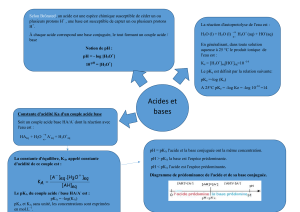
Réactions acido-basiques
I Autoprotolyse de l'eau
Inévitablement a lieu dans l'eau pure l'équilibre dépendant de la température: H2O H++ OH-
La loi d'action de masse s'écrit pour cet équilibre: [H+][OH-]/c°2 = Ke produit ionique de l'eau.
On écrit souvent [H+][OH-] = Ke(mais les concentrations doivent alors être prises en mol L-1), et même, en
posant h = [H+] et oh = [OH-]: h oh = Ke. On retiendra Ke = 10-14 à 25 °C.
La loi de Van't Hoff (établie en 2nde année) donne la dépendance de Ke avec T :
d(lnKe)/dT = rH°/RT2, où l'enthalpie de réaction rH° = 55,8 kJ mol-1 > 0 (réaction endothermique).
Cela montre que Ke est une fonction croissante de T (et pKe décroissante).
On retiendra qu'à 25 °C, pH + pOH = pKe= 14
avec pH = - log h et pOH = - log oh
Pour l'eau pure h = oh = Kesoit pH = pOH = ½ pKe = 7
Solution acide: h > oh et pH < 7.
On pourra négliger oh devant h si h  10 oh, soit pH  pOH - 1 = 14 - pH -1 soit oh << h si pH  6,5
Solution basique: oh > h et pH > 7.
h est négligeable devant oh si h  10 oh, pH  pOH + 1 = 14 - pH +1 soit h << oh si pH  7,5 (pOH  6,5)
II Couples acido-basiques
1 Constante d'acidité
Considérons le couple AH/A-: AH + H2O A- + H3O+
L'acide AH est le donneur de proton, sa base conjuguée A- est l'accepteur.
Si l'on note Ka la constante d'équilibre (constante d'acidité) de cette réaction, la loi d'action de masse s'écrit:
KA H O
AH c h A AH
a
[ ][ ]
[ ] [ ] [ ]
3
soit
[ ]
[ ]
AH
A
h
Ka
ou encore:
pH pK A
AH
a
log [ ]
[ ]
Un acide est d'autant plus fort que son pKa est petit
2 Constante de basicité
Considérons le couple BH+/B : B + H2O BH+ + OH-
La base B est l'accepteur de proton, son acide conjugué BH+ est le donneur.
On définit également la constante d'équilibre de cette réaction Kb (constante de basicité).
La loi d'action de masse s'écrit:
KBH OH
B c
oh BH
B
b
[ ][ ]
[ ]
[ ]
[ ]
soit
[ ]
[ ]
B
BH
oh
Kb
ou encore:
pOH pK BH
B
b
log[ ]
[ ]
Une base est d'autant plus forte que son pKb est petit
A 25°C, pour un couple AH/A- donné, on obtient:
AH + H2O A- + H3O+ : Ka = h[A-]/[AH] et A- + H2O AH + OH-: Kb = oh[AH]/[A-]
Par suite en faisant le produit : KaKb= h oh = Ke = 10-14 (25°C°) soit pKa+ pKb= 14 (à 25°C)
Il suffit donc d'une constante (acidité ou basicité) pour caractériser un couple.
Plus un acide est fort, plus sa base conjuguée est faible.
3 Cas de l'eau
Les couples sont: H3O+/H2O : H3O+ + H2O H2O + H3O+ Ka = 1 ; pKa = 0
H2O/OH- : H2O + H2O OH- + H3O+ Ka = Ke ; pKa = 14
Exercice: calculer le pKbdes couples de l'eau.
t (°C)
0
25
50
100
Ke
1,00 10-15
1,00 10-14
5,50 10-14
5,50 10-13
pKe
15,00
14,00
13,26
12,26
pH
7,50
7,00
6,63
6,13
pKe
12,0
12,5
13,0
13,5
14,0
14,5
15,0
0 20 40 60 80 100
t (°C)

Réactions acido-basiques - PCSI 2/5
4 Echelle d'acidité
Les acides plus fort que H3O+ (dont le pKa est inférieur à celui de H3O+: pKa < 0), réagissent totalement sur elle:
AH + H2O A- + H3O+K = Ka > 1
Ils ne peuvent donc pas exister dans l'eau.
Exemple : les deux acides forts HNO3 et HCl n'existent pas dans l'eau et manifestent (aux mêmes concentrations)
les mêmes propriétés acides (celles des acides forts). L'acide le plus fort qui puisse exister dans l'eau est H3O+.
On dit qu'il y a, pour les acides de pKa < 0, nivellement de la force des acides par l'eau.
De même, les bases plus fortes que HO- (dont le pKb est inférieur à celui de OH-: pKb < 0, soit pKa > 14 pour
l'acide conjugué), réagissent totalement sur elle: A- + H2O AH + HO-K = Kb > 1
Elles ne peuvent donc pas exister dans l'eau. La base la plus forte qui puisse exister dans l'eau est HO-.
Exemple : les deux bases fortes NH2- et H3CCH2O- n'existent pas dans l'eau et manifestent (aux mêmes
concentrations) les mêmes propriétés basiques (celles des bases fortes).
On dit qu'il y a, pour les bases de pKb < 0, nivellement de la force des bases par l'eau.
5 Domaines de prédominance
a Cas d'un monoacide AH A- pH
0 -1 pKa +1 14
La formule donne directement: [A-] < [AH]/10 pH < pKa- 1 domaine de prédominance de l'acide
[AH] < [A-]/10 pH > pKa + 1 domaine de prédominance de la base
Domaine intermédiaire, on ne peut négliger [AH] ni [A-] devant l'autre espèce.
b Cas d'une monobase B BH+pOH
0 -1 pKb +1 14
De même: [BH+] < [B]/10 pOH < pKb- 1 domaine de prédominance de la base
[B] < [BH+]/10 pOH > pKb + 1 domaine de prédominance de l'acide
Domaine intermédiaire: on ne peut négliger [BH+] ni [B] devant l'autre espèce.
c Cas d'un diacide
AH2 + H2O AH- + H3O+couples AH2/AH- et AH-/A2-:
AH- + H2O A2- + H3O+
AH2 AH- A2- pH
0 -1 pKa1 +1 -1 pKa2 +1 14
[A2-] et [AH-] << [AH2]pH < pKa1 - 1 domaine de prédominance du diacide
[A2-] et [AH2] << [AH-]pKa1 + 1 < pH < pKa2 - 1 domaine de prédominance de l'ampholyte
[AH2] et [AH-] << [A2-]pH > pKa2 + 1 domaine de prédominance de la dibase
d Cas d'une dibase
Refaire de même avec la dibase (couples B/BH+ et BH+/BH2+).
pH pK A
AH
a
log [ ]
[ ]
pOH pK BH
B
b
log[ ]
[ ]
KAH H O
AH
a1 3
2
[ ][ ]
[ ]
KA H O
AH
a2
23
[ ][ ]
[ ]

Réactions acido-basiques - PCSI 3/5
6 Diagramme de répartition des espèces
Considérons un diacide AH2 de constantes d'acidité K1et K2.
Introduisons dans une solution, une concentration totale c0initiale en AH2, AH-, A2-. On suppose qu'on peut faire
varier le pH de cette solution.
On définit les coefficients de répartition (sans unités) comme étant les pourcentages des différentes formes du
diacide (0 = [AH2]/c0,1 = [AH-]/c0,2 = [A2-]/c0)en solution. L'indice correspond à la charge de l'espèce.
Ces coefficients peuvent s'exprimer uniquement en fonction de h = [H3O+] et des constantes d'acidité.
Dans l'équation de conservation du diacide, on met en facteur l'espèce dont on veut calculer le coefficient i, en
tenant compte des lois d'action de masse pour chaque acidité:
[ ]
[ ]
AH
AH
h
K
2
1
[ ]
[ ]
AH
A
h
K
22
. Ainsi:
c0 = [AH2] + [AH-] + [A2-] =
[ ]( [ ]
[ ] [ ] [ ]) [ ]( )AH AH AH A AH AH K h
K K
h
22
2
221 1 2
2
1 1    
Soit
01 1 2
2
1
1
K
h
K K
h
de même:
1
1
1 1 2
2
1
K
h
K
h
K K
h
;
2
1 2
2
1 1 2
2
1
K K
h
K
h
K K
h
Ces relations sont très utiles, et généralisables aux polyacides, polybases, complexes...
Certains logiciels tracent les courbent i en fonction du pH. On obtient les figures suivantes
L'allure des courbes dépend beaucoup de l'écart entre les deux pK.
Pour des pK éloignés, pour pH < pK2- 1 on peut
négliger [A2-] devant les autres espèces. En
particulier pour pH = pK1, on obtient [AH-] = [AH2],
c'est-à-dire 0= 50%
Par contre, si les deux pK sont très proches (3ème
figure), les domaines de prédominance des espèces
s'interpénètrent, et pour pH = pK1, il n'est pas
possible de négliger [A2-] devant les autres espèces,
par suite 0 50 %.
7 Les calculs classiques de pH
Il faut savoir calculer le pH des solutions dans les cas
simples :
Mono (ou poly) acide (base) fort. Mono (ou poly) acide (base) faible. pH d'un ampholyte.
pH d'un mélange d'acides (de bases), d'un mélange d'acide et de base en proportion différente (ou égale) de celle
de l'équivalence. NE PAS RETENIR CES FORMULES MAIS LE PRINCIPE DU CALCUL.

Réactions acido-basiques - PCSI 4/5
8 Dosages acido-basiques
a Monoacide faible par base forte Bécher: AH (c0, v0). Burette: soude (Na+ OH-) (c, v versé)
Réactions chimiques (toutes les bases du milieu sur tous les acides du milieu):
(1) AH + H2O A- + H3O+constante d'équilibre Ka
(2) 2 H2O H3O+ + OH-constante d'équilibre Ke = 10-14
(3) AH + OH- A- + H2O constante d'équilibre:
KA
AH oh A h AH oh ohK
K
K
e
a
e
[ ]
[ ] [ ] [ ]
Dans le cas d'un acide plus fort que H2O (Ka >> Ke, soit pKa < 14): K >> 1 (et K >> Ka). La réaction (3) est celle
de plus grande constante d'équilibre, c'est elle qui influence le plus fortement les concentrations à l'équilibre, on
l'appelle réaction prépondérante (réaction qui supposée être le seul équilibre du milieu, conduit à une valeur
correcte des concentrations des espèces et en particulier du pH).
Attention, elle n'est prépondérante toutefois que si les réactifs (ici AH et OH- existent dans la solution), c'est-à-
dire avant l'équivalence), (et voir plus bas, s'il n'y a pas beaucoup d'ions H3O+dûs à la dissociation dès le départ de
l'acide AH, qui réagiraient avec OH- suivant (2) (sens 2) avec une constante d'équilibre très grande 1/Ke= 1014)
Plus généralement la réaction prépondérante R.P. est (lorsqu'ils existent) l'acide le plus fort avec la base la plus
forte du milieu.
Réaction du dosage: c'est la réaction prépondérante ayant lieu avant l'équivalence AH + OH- A- + H2O K
Elle est dite totale si sa constante K > 102 (par exemple), c'est-à-dire pKa < 12.
Equivalence: Moment où l'on a introduit les réactifs de la réaction du dosage dans les proportions
stoechiométriques. Le volume à l'équivalence est alors: ve = c0v0/c
On introduit le nombre sans dimension x = v/ve = cv/c0v0 = quantité de soude versé/quantité d'acide au départ
Calculs (très classiques, les approximations faites ici ne sont pas toujours valables):
x = 0: pH d'un acide (fort ou faible)
0 < x < 1: l'acide est en excès, la base en défaut. Si la réaction de dosage est totale, on peut écrire, à l'équilibre:
pH = pKa+log[A-]/[AH] avec [A-] = cv/(v+v0) et [AH] = (c0v0- cv)/(v+v0) soit pH = pKa+log[cv/(c0v0- cv)].
D'où la formule d'Henderson
pH pK xx
a
log1
(0<x<1) (formule indépendante de c0)
Cette formule n'est valable que suffisamment loin de 0 et de 1, et d'autant plus valable que les ions H3O+en début
de dosage sont en faible quantité (pour avoir une R.P. = (3) ), ce qui correspond à des solutions suffisamment
concentrées (voir exercices)
En particulier, lorsqu'elle s'applique, on peut écrire
pH pKa
à la demi équivalence (x = 0,5, alors [AH]=[A-]).
x = 1: pH d'une solution de (Na+ A-) c'est-à-dire de la base faible A- de pKb = 14-pKa à la concentration
c0v0/(v+ve).
x > 1: il y a excès d'ions OH-, d'où oh = (cv - cve)/(v+v0)
pH = 14 + log c v / (v + v ) + log(x -1)
0 0 0
(x>1)
Voici les courbes obtenues :

Réactions acido-basiques - PCSI 5/5
Les deux premiers exemples (acide fluorhydrique:
pKa = 3,2, acide acétique pKa = 4,75) sont des acides
moyennement faibles.
On voit, d'après le diagramme de répartition, qu'au
début du dosage (v = 0), il y a déjà une quantité de base
conjuguée, donc des ions H+ à doser (par (2) en
inverse). Le pH n'est pas rigoureusement pKa à la demi-
équivalence surtout pour HF. Par contre la vague de pH
à l'équivalence est grande.
Pour l'acide très faible de pKa = 9, par contre, il ne
s'est pas dissocié du tout à v = 0, et la relation
pH(ve/2)= pKa est rigoureusement vérifiée. Le saut de
pH est très faible et il sera difficile de doser un tel
acide.
b Monobase faible par acide forte Bécher: B (c0 v0). Burette: HCl (c, v versé)
Le traitement est le même. On retrouve pOH = pKb à la demi-équivalence soit encore pH = pKa.
c Polyacide faible par base forte Bécher: acide phosphorique H3PO4 (c0, v0). Burette: soude (c, v versé)
Il y a ici trois acidités de constante pK1 = 2,2; pK2 = 7,2; pK3 = 12,3, donc trois équivalences.
On note ve le volume de la première équivalence et on pose x = v/ve.
On étudie les cas suivants: x = 0; 0 < x < 1; x = 1; 1 < x < 2; x = 2; 2 < x < 3; x = 3; x > 3.
Le troisième saut de pH est très faible: on ne peut pas
observer la troisième acidité de cet acide grâce à un
indicateur coloré.
On remarque que seule la deuxième demi-
équivalence vérifie la formule pH = pK2.
La première demi équivalence acidité ne la vérifie
pas car la première acidité est forte, il n'y a pas de
R.P. il faut tenir compte de (2) et (3).
La dernière demi équivalence non plus car la réaction
de neutralisation de la deuxième acidité est de
constante trop faible et n'est pas totale. C'est d'ailleurs
pourquoi on n'observe pas de saut visible de pH lors
de la troisième équivalence.
9 Solutions tampons
Ce sont des solutions dont la propriété est d'avoir un pH variant très peu par addition d'un acide d'une base ou
d'eau (dilution).
Le pouvoir tampon est défini par
tdc
dpH
B
où dpH est la variation du pH de la solution obtenue lors de la
variation de la concentration dcB d'une base forte introduite dans la solution.
On obtient une solution tampon en mélangeant un acide faible AH avec une solution d'un de ses sels (de sodium
par exemple: ANa soit A-,Na+) dans des proportions correspondant au domaine d'Henderson du dosage acide
faible AH par base forte (soude). En effet, dans cette partie la pente de la courbe pH(v) est très faible.
pH = pKa+log(x/(1-x)) soit dpH/dx =1/2,3 [1/x + 1/(1-x)] = 1/2,3x(1-x).
Or cB = c x, par suite t = 2,3 c x (1 - x) est maximum pour x = 0,5 (demi équivalence).
Par dilution, le pH varie peu, mais t diminue (effet de c).
Les pseudo-tampons sont des solutions:
peu sensibles à la dilution mais sensibles à l'adjonction de base ou d'acide (cas des ampholytes, car ils
correspondent à l'équivalence d'un dosage)
ou encore peu sensibles aux acides et aux bases mais sensibles à la dilution (cas des acides forts).