ISOSTATISME (cours)

ISOSTATISME (cours)
1.- Degrés de liberté(de mobilité) :
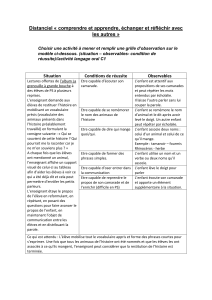
Exemple : Etude de la massue lancée par un jongleur.
y1
z1
O1
x
1
y
x
O
z
Examinons les mouvements d’une massue par rapport au sol. Cette étude nécessite la mise en place de deux
repères :
- un repère R (O, x
r
, y
r
, z
r
) lié au sol et considéré fixe
r
- un repère R1 (O1, x
r
1, y1, z
r
1) lié à la massue.
Tout mouvement, même complexe, du repère R1 (lié à la massue) par rapport au repère R (lié à la terre) peut se
décomposer au plus en :
* 3 translations :
- une translation suivant (0, )x
r
notée Tx ;
r
- une translation suivant (0, )y notée Ty ;
r
- une translation suivant (0, )z notée Tz ;
* 3 rotations :
- une rotation autour de (0, )x
r
notée Rx ;
r
- une rotation autour de (0, )y notée Ry ;
r
- une rotation autour de (0, )z notée Rz ;
Ces six possibilités de mouvement sont appelées « degrés de liberté » ou degrés de mobilité.
Tout solide possède au plus 6 degrés de liberté (ou 6 degrés
de mobilité)
3 degrés de liberté en translation
3 degrés de liberté en rotation
suivant et autour des 3 axes d'un trièdre.
Noguet Lycée Blaise Pascal Colmar Isostatisme cours.doc 17/02/09 1/3

2.- Liaisons :
2.1.- Qu est ce qu'une liaison ?
Réaliser une liaison mécanique entre deux pièces c’est supprimer un ou plusieurs degrés
de liberté.
Chaque fois qu’on supprime un degré de liberté on dit qu’on établit un degré de liaison.
Si on supprime une seule fois le même degré de liberté alors le système de liaison est dit isostatique.
Si on supprime plusieurs fois le même degré de liberté alors le système de liaison est dit hyperstatique.
2.2. - Torseur cinématique :
Une liaison peut autoriser un certain nombre de mouvements c'est-à-dire laisser subsister un certain nombre de
degré de liberté.
A chaque degré de liberté on associe un paramètre (grandeur physique) de vitesse.
Ainsi : pour les translations on associe des paramètres de vitesse linéaire (v en m/s)
- à la translation Tx on associe la composante de vitesse linéaire vx ;
- à la translation Ty on associe la composante de vitesse linéaire vy ;
- à la translation Tz on associe la composante de vitesse linéaire vz .
pour les rotations on associe des paramètres de vitesse angulaire (ω en rad/s) :
- à la rotation Rx on associe la composante de vitesse angulaire ωx ;
- à la rotation Ry on associe la composante de vitesse angulaire ωy ;
- à la rotation Rz on associe la composante de vitesse angulaire ωz.
Ces paramètres, vitesse linéaire VA
r
et vitesse angulaire
Ω
r
, sont des grandeurs vectorielles dont les
composantes respectives sont vx. , vy, et vz pour le vecteur vitesse linéaire VA
r
et ωx , ωy , ωz. pour le vecteur
vitesse angulaire Ω
r
.
Ces 6 paramètres constituent les éléments de réduction au point A (A = centre de la liaison) du torseur
cinématique associés à la liaison étudiée :
{V 1/2 }A =
ω
ω
ω
Z
Y
X
Z
y
X
Av
v
v
) Application : Ecrire le torseur cinématique de chaque liaison en complétant le tableau.
2.3.- Torseur statique ou d'action mécanique transmissible :
Une liaison peut transmettre un certain nombre d'efforts en supprimant certain degrés de liberté.
A chaque degré de liberté supprimé on associe un paramètre (grandeur physique) d'effort.
Ainsi : pour les translations supprimées par la liaison on associe des paramètres de force (F en N)
- à la suppression de la translation Tx on associe la composante de force X ;
- à la suppression de la translation Ty on associe on associe la composante àe force Y ;
- à la suppression de la translation Tz on associe on associe la composante de force Z.
pour les rotations supprimées on associe des paramètres de moment (MA en Nm)
- à la suppression de la rotation Rx on associe la composante de moment L ;
- à la suppression de la rotation Ry on associe la composante de moment M ;
- à la suppression de la rotation Rz on associe la composante de moment N.
Ces paramètres, force F
r
et moment M
r
A sont des grandeurs vectorielles dont les composantes respectives sont
X, Y, Z pour le vecteur force F
r
et L, M, N pour le vecteur moment M
r
A.
Ces 6 paramètres constituent les éléments de réduction au point A (A = centre de la liaison) du torseur d'action
mécanique transmissible par la liaison étudiée :
{T 1/2 }A =
N
M
L
Z
Y
X
A
) Application : Ecrire le torseur d'action mécanique transmissible de chaque liaison en complétant le
tableau.
Noguet Lycée Blaise Pascal Colmar Isostatisme cours.doc 17/02/09 2/3

2.4.- Liaisons parfaites :
Lors de l'écriture des différents torseurs vous avez considéré des liaisons parfaites, c'est-à-dire sans jeu et sans
frottement. La géométrie des surfaces en contact à également été considérée parfaite.
1 1
0 0
0 0
Pivot glissant
Zone de contact
prismatique Glissière
0 0
0 1
0 0
Quelconque Encastrement
1 0
0 1
0 1
Zone de contact
plane Appui plan
Zone de contact
linéaire rectiligne
Linéaire
rectiligne
0 1
1 1
1 0
Zone de contact
sphérique +
p
onctuelle
Sphérique
à doi
g
t
1 0
0 0
1 0
R T
0 0
0 0
0 0
Représentation
3D
Représentation
2D
Degrés de mobilité
Type de contact
1 0
1 1
1 0
Linéaire
annulaire
Zone de contact
linéaire annulaire
1 1
1 1
1 0
Zone de contact
ponctuelle
Ponctuelle
0 0
1 0
0 0
Zone de contact
cylindrique + arrêts
axiaux (surfaces de
contact planes ou
p
onctuelles
)
.
Pivot
0 0
1 1
0 0
Zone de contact
hélicoïdale Hélicoïdale
Zone de contact
sphérique Rotule
1 0
1 0
1 0
Zone de contact
cylindrique
Nom de la liaison
Noguet Lycée Blaise Pascal Colmar Isostatisme cours.doc 17/02/09 3/3