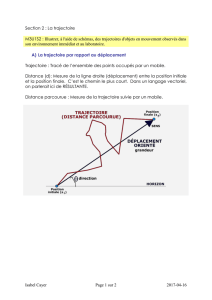
p e + 1 p 1 - e p 1 - e² Si E = - k / 2mC², la trajectoire est circulaire. III

Leçon 150 : Mouvement à accélération centrale
Pré requis : Cinématique du point en coordonnées
polaires ; principes de la dynamique du point.
Propriétés des coniques.
Dans toute la leçon, M est un point matériel de masse
m. Tous les référentiels sont supposés Galiléens.
I Les forces centrales et la loi des aires
Def Une force est dite centrale si elle est portée
par avec O le centre du repère.
Exemples :
● Une bille de masse m qui a un mouvement plan
sans frottement est attachée à une ficelle sans masse
qui coulisse dans un trou O au centre du plan.
● L’oscillateur spatial isotrope.
● Force Newtoniennes d’interaction entre deux
particules :
Interaction gravitationnelle : = –
Interaction électrostatique : =
Conservation du moment cinétique - loi des aires
Dans un mouvement de force centrale :
a) Le mouvement est plan. Il va porter et
b) La quantité r² est une constante appelée constante
des aires.
Le b) équivaut à dire que l’aire balayée par par unité
de temps est constante.
II Les mouvements à force centrale
conservatrice newtonienne :
Conservation de l’énergie mécanique qui peut
s’écrire :
E = mr² +
mC²
2r²
+Ep(r) avec C = r² = cste
Epeff(r)
Exemples d’énergies potentielles newtoniennes
effectives :
Interaction newtonienne Interaction newtonienne
répulsive attractive
Etude du mouvement pour les interactions
newtoniennes
Propriété : La trajectoire de la particule est une
conique de foyer O dont l’équation est :
R = – ε avec p = , ε = 1 et
e = , ( = 0 pour t = 0)
● Si E = 0 :
La trajectoire est une
parabole
rmin =
p
2
● Si E < 0 : état lié
La trajectoire est une ellipse
rmin =
p
e + 1
(apogée) ;
rmax =
p
1 - e
(périgée)
a =
p
1 - e²
; b²= pa
● Si E = - k / 2mC², la trajectoire est circulaire.
III Applications
● Les trois lois de Kepler :
1) Les planètes décrivent des ellipses autour du soleil
2) Les trajectoires suivies vérifient la loi des aires
3) Le cube du demi grand axe est proportionnel au
carré de la période de révolution.
● Les vitesses cosmiques : ce sont des vitesses de
lancement au niveau de la terre :
Vitesse d’une trajectoire circulaire au niveau de la
terre : v1 =
G Mt
r
≈ 28 000km/h
Vitesse de libération de l’attraction terrestre :
v2 =
2 G Mt
r
≈ 39 600km/h
● Mise en orbite géostationnaire d’un satellite en
utilisant une orbite de transfert.
● Les voyages interplanétaires et la fronde
gravitationnelle.
Source : Pascal Brasselet Mécanique PCSI/MPSI-puf
.
.
● Si ε =1 : interaction
répulsive :
La trajectoire est une branche
d’hyperbole
(la plus éloignée de O)
rmin =
p
e - 1
; a =
p
e² - 1
;
b²= pa
● Si ε = – 1 : interaction
attractive :
● Si E > 0 : état libre ;
La trajectoire est une
branche d’hyperbole
(la plus proche de O)
rmin =
p
e + 1
.