Programme des colles de chimie PC*

Programme des colles de chimie PC*
Semaine 1 : du 15 au 19 septembre 2014
1 Changements d’état isobares des mélanges binaires
1.1 Notions et contenus
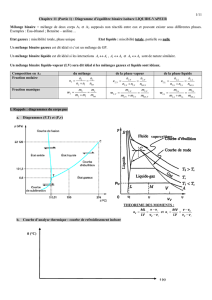
Diagrammes isobares d’équilibre liquide- vapeur :
— avec miscibilité totale à l’état liquide
— avec miscibilité nulle à l’état liquide
— avec miscibilité partielle à l’état liquide.
Diagrammes isobares d’équilibre solide-liquide :
— avec miscibilité totale à l’état solide,
— avec miscibilité nulle à l’état solide, avec ou sans composé défini à fusion congruente
— avec miscibilité partielle à l’état solide.
Théorème des moments chimiques.
Variance : nombre de degrés de liberté d’un système à l’équilibre.
1.2 Capacités exigibles (à évaluer en priorité)
Mettre en œuvre une distillation fractionnée à la pression atmosphérique et une hydrodistillation ou une distillation
hétéroazéotropique. (TP pas encore réalisé)
Construire un diagramme isobare d’équilibre entre deux phases d’un mélange binaire à partir d’informations
relatives aux courbes d’analyses thermiques.
Décrire les caractéristiques des mélanges homoazéotropes, hétéroazéotropes, indifférents, eutectiques et des com-
posés définis.
Dénombrer les degrés de liberté d’un système à l’équilibre et interpréter le résultat. Exploiter les diagrammes
isobares d’équilibre entre deux phases pour, à composition en fraction molaire ou massique donnée :
— tracer l’allure de la courbe d’analyse thermique en indiquant le nombre de degrés de liberté du système sur
chaque partie de la courbe ;
— déterminer les températures de début et de fin de changement d’état ;
— donner la composition des phases en présence à une température T fixée ainsi que les quantités de matière ou
les masses dans chaque phase.
Interpréter une distillation simple, une distillation fractionnée, une distillation hétéroazéotropique à l’aide des
diagrammes isobares d’équilibre liquide-vapeur.
1.3 Commentaires
L’étude thermodynamique des équilibres n’est pas encore vue. Aucun calcul relatif aux équilibres entre phases ne
peut être demandé : le potentiel chimique n’est pas vu, les grandeurs thermodynamiques de réaction non plus. On se
limite donc au tracé expérimental et à la lecture des diagrammes.
La règle de Gibbs ou règle des phases n’est plus au programme. Le calcul de la variance est effectué de la manière
suivante : v=X−Yavec Xnombre de paramètres intensifs (P,T, fractions molaires) et Yle nombre de relations
entre ces paramètres (somme des fractions molaires = 1 dans chaque phase, conditions d’équilibre). Une distinction
a été effectuée entre le calcul général de la variance et le calcul du nombre de degrés de liberté d’un système précis
pour lequel des contraintes supplémentaires ont été imposées (état initial particulier, pression fixée, systèmes dans des
conditions azéotropiques. . .).
1

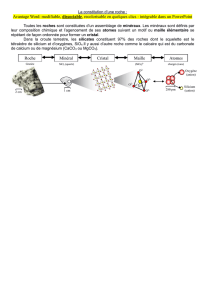
2 Solides cristallins (révisions de première année)
2.1 Notions et capacités exigibles
Modèle du cristal parfait : description du cristal parfait, population, coordinence, compacité, masse volumique.
Limites du modèle du cristal parfait. Décrire un cristal parfait comme un assemblage de mailles. Déterminer la
population, la coordinence et la compacité pour une structure fournie. Déterminer la valeur de la masse volumique
d’un matériau cristallisé selon une structure cristalline fournie. Relier le rayon métallique, cavalent, de Van der Waals
ou ionique, selon le cas, aux paramètres d’une maille donnée. Confronter des données expérimentales aux prévisions
du modèle.
Métaux et cristaux métalliques : description des modèles d’empilement compact de sphère identiques. Maille
conventionnelle cubique à faces centrées et ses sites interstitiels. Alliages de substitution et d’insertion. Localiser les
interstices tétraédriques et octaédriques entre les plans d’empilement. Localiser, dénombrer les sites tétraédriques et
octaédriques d’une maille CFC et déterminer leur habitabilité. Relier les caractéristiques de la liaison métallique (ordre
de grandeur énergétique, non directionnalité) aux propriétés macroscopiques des métaux. Citer des exemples d’alliage
et leur intérêt par rapport à des métaux purs. Prévoir la possibilité de réaliser des alliages de substitution ou d’insertion
selon les caractéristiques des atomes mis en jeu.
Solides macrocovalents et moléculaires. Identifier les liaisons covalentes, les interactions de Van der Waals et les
liaisons hydrogène dans un cristal de structure donnée. Relier les caractéristiques des liaisons de Van der Waals et
des liaison hydrogène (directionnalité ou non, ordre de grandeur des énergies mises en jeu) et les propriétés macro-
scopiques des solides correspondants. Comparer les propriétés macroscopiques du diamant et du graphite et interpréter
les différences en relation avec les structures microscopiques (structures cristallines fournies).
Solides ioniques. Relier les caractéristiques de l’interaction ionique dans le cadre du modèle ionique parfait (ordre
de grandeur de l’énergie d’interaction, non directionnalité, charge localisée) avec les propriétés macroscopiques des
solides ioniques. Vérifier la tangence anion-cation et la non tangence anion-anion dans une structure cubique de type
AB fournie, à partir des valeurs du paramètre de maille et des rayons ioniques.
2.2 Commentaires
Par rapport au programme précédent, aucune structure n’est à connaître sauf la maille conventionnelle cubique à
faces centrées. Toute autre maille devra être donnée dans l’énoncé par un schéma ou une description complète.
2