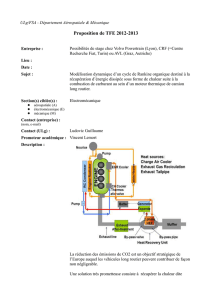
Applications des eclt_irrotationnels 09

1
1
Elémentsdemécani
q
uedesfluides
.
be
q
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
2
• Etude de solutions analytiques d’écoulement potentiel
• Utilisation du principe de superposition
– Écoulement irrotationnel complexe
Vortex libre
Objectifsdelaséance
.
be
–
Vortex
libre
– Génération de « corps » imperméable
– Couche tourbillonnaire - utilité
• Portance et traînée en écoulement irrotationnel
– Effet Magnus-Robbin
– Quantification de la portance – liaison à l’amplitude de la circulation
–
Paradoxe de d
’
Alembert
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
Paradoxe
de
dAlembert
• Modélisation de corps complexes
– Problème direct et indirect
– Transformation conforme
– Application aux ailes d’avion

2
3
Solutionsanalytiques
.
be
d’écoulementsirrotationnels
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
4
• Coordonnées polaires
Rappelmathématique:Coordonnéespolaires
()
(
)
x
yz r z θ →
y
⎧
⎛⎞
.
be
cos
sin
xr
yr
θ
θ
=
⎧
⎨=
⎩
wv uw vu
⎡⎤
⎛⎞ ⎛⎞
∂∂ ∂∂ ∂∂
⎛⎞
(
)
rz
Uvvv
θ
=
22
Atan
y
x
rxy
θ
⎧
⎛⎞
=
⎜⎟
⎪⎝⎠
⎨
⎪=+
⎩
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
,,
wv uw vu
Uyz zx xy
⎡⎤
⎛⎞ ⎛⎞
∂∂ ∂∂ ∂∂
⎛⎞
∇× = − − −
⎢⎥
⎜⎟ ⎜⎟
⎜⎟
∂∂ ∂∂ ∂∂
⎝⎠
⎝⎠ ⎝⎠
⎣⎦
(
)
11
,,
zrz r
rv
v
vvv v
Urzzrrr
θ
θ
θ
θ
⎡⎤
⎛⎞
∂
∂
∂∂∂ ∂
⎛⎞
⎛⎞
∇× = − − −
⎢⎥
⎜⎟
⎜⎟
⎜⎟ ⎜⎟
∂∂ ∂∂ ∂ ∂
⎝⎠
⎝⎠
⎢⎥
⎝⎠
⎣⎦

3
5
• Les deux équations
pour un fluide incompressible en stationnaire
ou
non
Rappel:Deuxéquationssimilaires…
0ΔΨ =
.
be
pour
un
fluide
incompressible
en
stationnaire
ou
non
isopotentielle
ligne de courant
0
φ
Δ=
constante
φ
tt
Ψ
;
uv
∂
Ψ∂Ψ
==
−
;uv
x
y
φ
φ
∂
∂
==
∂
∂
en 2D
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
ligne
de
courant
cons
t
an
t
e
;
uv
yx
==
∂
∂
en
2D
6
• L’équation de Laplace est linéaire et donc le principe de
superposition est d’application
Principedesuperposition
20
ff
∇
=Δ =
.
be
•
La combinaison de solutions simples peut permettre
()
2
22
0
0
ff
gg
mfg
mfg
∇=Δ=
=+
∇
=∇ + =
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
La
combinaison
de
solutions
simples
peut
permettre
d’envisager des écoulements complexes

4
7
• Types d’écoulements irrotationnels principaux en 2D:
Typesd’écoulementsirrotationnelsprincipaux
.
be
– Champ de vitesse uniforme
– Source ou puits
–Vortex
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
8
• Définition du problème :
– Écoulement 1D selon x
– vitesse caractéristique à l’infini
Solutionsanalytiques:Champdevitesseuniforme
0
U
U
∞
⎛⎞
=⎜⎟
⎝⎠
U∞
.
be
• Solutions :
– En terme de fonction de courant :
–
En terme de
p
otentiel de vitesse :
0
uU y
v
x
ψ
ψ
∞
∂
⎧==
⎪
∂
⎪
⎨
∂
⎪==−
⎪
∂
⎩
uU
x
φ
∞
∂
⎧==
⎪
∂
⎪
⎨
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
p
Uy
Ux
ψ
φ
∞
∞
=
⎧
⎨=
⎩
lignes de courant horizontales
isopotentielles verticales
0vy
φ
⎨
∂
⎪==
⎪∂
⎩

5
9
Solutionsanalytiques:Champdevitesseuniforme
.
be
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
10
• Définition du problème :
– Source : apport ponctuel
– Puits : retrait ponctuel
–
P
os
i
t
i
o
n
:
(0,0)
Solutionsanalytiques:Source/Puits
.
be
os t o
: (0,0)
– Débit spécifique [m²/s] : Q
– Problème symétrique Æsolution symétrique
– Il est préférable de travailler en coordonnées cylindriques
• Solutions :
– Puisque la solution est symétrique, le débit est conservée sur
l’ensemble des cercles centrés en (0,0)
ArGEnCo – MS²F‐ Hydrologie,HydrodynamiqueAppliquéeetConstructionsHydrauliques(HACH)
http://www.hach.ulg.ac
.
– Définition de l’intensité de la source/puits :
2
Q
mb
π
=± Débit total
périmètre du tube d’injection/retrait
par symétrie 2
rr r
CC
Qvds vds rv
π
===
∫∫