AVEC UN RAPPORTEUR… I) Définitions 1) angle Un angle est

A
B
C
AVEC UN RAPPORTEUR…
I) Définitions
1) angle
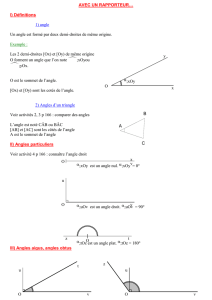
Un angle est formé par deux demi-droites de même origine.
Exemple :
Les 2 demi-droites [Ox) et [Oy) de même origine
O forment un angle que l’on note
;xOyou
;yOx.
O est le sommet de l’angle.
[Ox) et [Oy) sont les cotés de l’angle.
2) Angles d’un triangle
Voir activités 2, 3 p 166 : comparer des angles
L’angle est noté CÂB ou BÂC
[AB] et [AC] sont les côtés de l’angle
A est le sommet de l’angle
II) Angles particuliers
Voir activité 4 p 166 : connaître l’angle droit
;xOy est un angle nul.;xOy = 0°
;uOv est un angle droit.;uOv = 90°
;tOzest un angle plat.;tOz = 180°
III) Angles aigus, angles obtus
O
x
y
;xOy
O
y
x
O
u
v
O
z
t
O
u
v
O
u
v
t
z

;tOvest plus petit qu’un angle droit. ;vOzestplus grand qu’un angle droit.
On dit que c’est un angle aigu. On dit que c’est un angle obtus.
Sa valeur est comprise entre 0° et 90°. Sa valeur est comprise entre 90° et 180°.
IV) Mesure et construction d’un angle
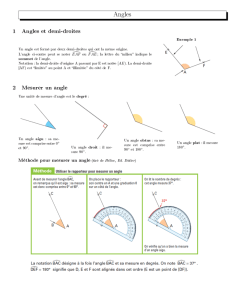
Le rapporteur n’est pas un instrument de tracé, mais un instrument de mesure.
Il est gradué en degrés (de 0° à 180°) ou en grades (0 à 200)
Souvent, le rapporteur est doté de deux graduations en degrés :
l’une que l’on appellera la graduation extérieure,
l’autre que l’on appellera la graduation intérieure.
Mesure
INSTRUMENPOCHE/Angle/Mesure d’un angle2
INSTRUMENPOCHE/Angle/Mesure d’un angle5
Construction
INSTRUMENPOCHE/Angle/Construction d’un angle1 (aigu)
INSTRUMENPOCHE/Angle/Construction d’un angle2 (obtu)
V) Bissectrice d’un angle
1) angles adjacents
Deux angles adjacents ont le même sommet, un côté commun et sont situés de part et d’autre de ce côté.
;zOyet ;yOx sont adjacents.
;zOxet ;zOy ne sont pas adjacents car ils ne sont pas de chaque côté du côté commun [Oz).
Graduation extérieure
extérieure« extérieure
»
Graduation intérieure
« intérieure »
Centre
x
y
O
z

(d)
x
y
A
B
2) bissectrice d’un angle
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles adjacents de même mesure.
[Oy) est la bissectrice de l’angle;xOz.
;xOy = ;yOz
AVEC UNE REGLE ET UNE EQUERRE…
I) Points et droites
1) Point
Voir activité : quelques tracés
A l’oral : leur dire de placer trois points que l’on nomme A, B et C. Relier les points A et B, B et C et A et C.
Voir ce qu’ils font et en faire passer plusieurs au tableau…
Un point est en général représenté par une croix. Sur une même figure, deux points distincts (différents) ne
portent pas le même nom.
Exemples :
2) Droites
Une droite se trace à l’aide d’une règle. On la représente par une partie d’elle-même car une droite est en fait
illimitée. Cela veut dire qu’elle ne se termine jamais et donc qu’on ne peut pas la mesurer.
représentation
nom
(d)
(xy)
(AB)
3) Points et droite
O
x
y
z
A
B

A
B
D
C
Voir l’activité : est ou n’est pas
Le point M est sur la droite (d). On dit que M appartient à (d) et on note M  (d).
Le point N n’est pas sur la droite (d). On dit que N n’appartient pas à (d) et on note N  (d).
II) Segment et milieu
1) Segment
Un segment est une portion de droite limitée par deux points. Il possède donc deux extrémités et il est donc
« mesurable ». Le segment d’extrémités A et B ci contre se note [AB]. La longueur du segment [AB] est notée
AB.
Exemple :
Construire un segment [AB] tel que AB = 5 cm
2) Milieu
Puisqu’un segment se mesure, on peut définir son milieu.
Définition
Le milieu d’un segment est le point de ce segment qui le partage en deux segments de même longueur.
Exemple :
On va placer I milieu de [AB]
Sur cet exemple, I est le milieu de [AB] et on a indiqué que AI = IB à l’aide du codage.
III) Demi-droite
Définition
Une demi-droite est une droite qui possède une extrémité et une seule (sinon c’est un segment)
Comme la droite, la demi-droite ne se mesure pas. Elle est, comme la droite, illimitée.
Par exemple voici les demi-droites [AB) et (CD]
A et D sont aussi appelés les origines des demi-droites.
IV) Position relative de deux droites
1) Droites sécantes
(d)
M
N
I
(d
)
(d’)
A
B
I
A
B
Codage
Codage

Définition :
Les droites (d) et (d’) se coupent (se croisent) en I. On dit qu’elles sont sécantes. I est leur point d'intersection,
c’est le seul point appartenant à la fois à (d) et à (d’).
2) Droites perpendiculaires
voir activité : perpendiculaires
INSTRUMENPOCHE/Constructionsdebases/perpendiculaire3
Définition :
Les droites (d) et (d’) se coupent en formant un angle droit (réalisé avec une équerre). On dit qu’elles sont
perpendiculaires.
On note : (d) (d’).
3) Droites parallèles
voir activité : parallèles
INSTRUMENPOCHE/Constructionsdebases/parallele2 ou 1
Définition :
Les droites (d) et (d’) n’ont pas de point d’intersection, même en les prolongeant indéfiniment. On dit qu’elles
sont parallèles.
On note : (d) // (d’)
Cas particulier :
Définition :
Les droites (d) et (AB) se superposent. On dit qu’elles sont confondues. (d) et (AB) sont aussi deux droites
parallèles. AVEC UN COMPAS…
I) Cercle
1) Définition
Un cercle est formé de tous les points situés à une même distance d’un point appelé centre. Cette distance est
appelée le rayon du cercle.
(d)
(d’)
Codage
(d’)
(d)
(d)
B
A
O
A
B
ray
on
diam
ètre
centre
corde