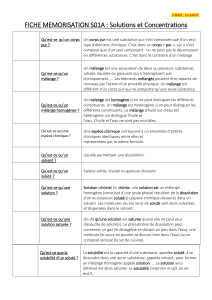
TD3 Potentiel chimique et solutions (2006-2007)

Potentiel chimique et Solutions
1) Influence de T et P sur le potentiel chimique :
a) Quelle est la différence entre le potentiel chimique de la vapeur d’eau à 100°C
sous 1 bar et celui de l’eau liquide à 95°C sous 1 bar ?
b) Supposons maintenant que la pression est de 1,2 105 Pa et la température 100°C.
Quelle est alors la nouvelle différence des potentiels chimiques entre le potentiel
chimique de la vapeur d’eau à 100°C sous 1 bar et celui de l’eau liquide à 100°C
sous 1,2 bar ?
c) Quelle est la différence entre le potentiel chimique de la vapeur d’eau à 100°C
sous 1,2 bar et sous 1 bar ?
Remarque : On considérera les gaz comme parfaits
Données : S°m(H2O,liq)=70 J.K-1.mol-1, supposée indépendante de T.
M(H2O) = 18 g.mol-1
2) Application de la loi de Henry :
Rappel : A température donnée, la quantité de gaz dissous à saturation (équilibre) dans un
liquide est proportionnelle à la pression du gaz au dessus de ce liquide
Proposer une explication des accidents de décompression en plongée.
Indication : penser à l’ouverture des bouteilles de boisson gazeuse.
Propriétés colligatives :
Lors de l'ajout d'un soluté à un corps pur largement majoritaire, on observe une élévation du
point d'ébullition, l'abaissement du point de fusion et l'existence d'une pression osmotique.
Ces propriétés des solutions diluées sont dites colligatives (signifiant "dépendant de
l'ensemble") car elles ne dépendent que des constantes physiques du corps pur largement
majoritaire et aucunement de celles du (ou des) constituant(s) ultra-minoritaire(s). Le (ou les)
constituants ultra-minortaire(s) intervien(nent) seulement par sa(leur) fraction molaire (ou une
grandeur de composition analogue) donc par son(leur) abondance relative dans une phase et
non par sa(leur) nature.
1) Caractéristiques communes aux propriétés colligatives
Dans la suite nous supposerons que le soluté n'est pas volatil et que le soluté ne se dissout pas
dans le solvant solide.
Toutes les propriétés colligatives ont leur origine dans la diminution du potentiel chimique du
solvant liquide associée à la présence du soluté. µa* pour le solvant pur est réduit à µa*+RTlnxa
en présence d'un soluté. Le soluté n'a pas d'influence directe sur le potentiel chimique de la
vapeur et du solvant solide d'après les hypothèses.

En utilisant le diagramme ci dessous montrer qu'il y a abaissement du point de fusion et qu'il
y a élévation du point d'ébullition.
2) Exemples d'application
a) L'osmose
Expérience préliminaire :
Π
A B
Il règne une pression extérieure de 1 bar et les fluides sont supposés incompressibles.
Initialement dans le compartiment gauche (A), on introduit de l'eau pure (composé 1). Dans le
compartiment droite (B), on introduit une solution 0,1 mol.L-1 de sulfate de cuivre(II) CuSO4
(composé 2) ; la solution du compartiment B est bleue. Les deux compartiments sont séparés
par une membrane de cellophane, semi-perméable, qui laisse diffuser le solvant eau mais pas
le soluté CuSO4.
1) On laisse l'équilibre s'établir : on observe une différence de hauteur entre les deux tubes.
La surpression Π observée est appelée pression osmotique. Expliquer. Quelle sera la
couleur de chaque compartiment à l'équilibre ?
2) Montrer que Π est proportionnelle à x2 et donner le coefficient de proportionnalité.
3) Montrer que l'on aboutit (après une approximation) à la loi de Van't Hoff Π = c2 RT
4) Application de l'osmose : l'osmométrie
L'influence de la pression étant facilement mesurable, l'une des applications les plus courantes
de l'osmométrie est la mesure des masses molaires des macromolécules (protéines et
polymères synthétiques). Ces énormes molécules donnant des solutions loin d'être idéales, on
suppose que l'équation de van't Hoff est seulement le premier terme du développement d'une
équation du viriel : Π = c2 RT{1+B c2 + …}
Les termes suivants tiennent compte de la non idéalité ; la constante empirique B est dite
coéfficient osmotique du viriel.
Potentiel chimique, µ
TfTeb

Exemple : La pression osmotique de solutions de PVC dans la cyclohexanone à 298 K est
donnée ci-dessous. La pression est exprimée en terme de hauteur de solution (de masse
volumique ρ = 0,980 g.cm-3). Déterminer la masse molaire du polymère.
c (g L-1) 1,00 2,00 4,00 7,00 9,00
h (cm) 0,28 0,71 2,01 5,10 8,00
5) Rôle de l'osmose en biologie :
Osmose : diffusion d'eau à travers une membrane sélectivement perméable d'une solution à
faible concentration de soluté, vers une solution à forte concentration de soluté.
Diffusion : tendance qu'ont les particules, molécules ou ions, à se disperser ou se déplacer
d'une zone de forte concentration vers une zone de faible concentration due à leur énergie
cinétique.
Commenter cette phrase entendue dans une émission d'ARTE : " […] Comme les humains,
tous les poissons ont donc besoin d'eau pour leur organisme. Mais pendant que les poissons
d'eau douce passent leur vie à essayer de se débarasser de toute l'eau qui entre en eux, les
poissons de mer doivent filtrer l'eau de mer. On pourrait donc dire pour simplifier que les
poissons de mer boivent, mais pas les poissons d'eau douce."
b) Abaissement du point de fusion, loi de la cryoscopie :
Détermination de la structure du soufre solide :
Le corps simple soufre à l’état solide est formé de molécules Sn.
On cherche à connaître la valeur de n à partir de mesures de températures de cristallisation.
Pour cela, on utilise du naphtalène : quand on dissout m2 = 0,95 g de soufre dans m1 = 52,21 g
de naphtalène, la température de cristallisation de ce dernier diminue de 0,49 °C.
On considèrera que le naphtalène et le soufre forment une solution idéale en phase liquide
alors que, en phase solide, les deux solides sont totalement immiscibles.
1) On exprimera la condition d’équilibre du constituant A1 présent simultanément dans la
phase solide et la phase liquide et on en déduira l’équation T(x1), x1 étant la fraction
molaire du composé 1, de la courbe appelée liquidus pour des systèmes dilués en A2,
A1 se comporte comme solvant. On montrera que cette expression de la température
est proportionnelle à x2 quand celui-ci tend vers 0 (loi de la cryoscopie).
2) Utiliser l’équation établie ci-dessus pour déterminer x2 puis la masse molaire M2 du
soufre et enfin, la valeur de n.
Données :
Caractéristiques du corps pur naphtalène :
Masse molaire : M = 128,2 g.mol-1 ;
Sous la pression totale P = 1 bar, température de cristallisation : 80,2 °C ;
Enthalpie molaire de fusion L1 = 19,1 kJ.mol-1 (considérée indépendante de la température).
Masse molaire atomique du soufre : M = 32,06 g.mol-1.
Constante des gaz parfaits : R = 8,314 J.K-1.mol-1.