CHIMIE - COURS 1-Préparation de Solution (2)

Chapitre I : Préparation de solutions
9
CHAPITRE I
PREPARATION DE
SOLUTIONS

Chapitre I : Préparation de solutions
10
I- Introduction:
La chimie est une science de la nature qui étudie la matière et ses transformations. La chimie des
solutions est la branche de la chimie qui s'intéresse à toutes les réactions en solution, car pour tout
chimiste digne de ce nom, il est indispensable de savoir préparer des solutions pour des
concentrations déterminées. La chimie des solutions s'intéresse aux solutions solides et liquides
mais surtout liquides.
Afin de cerner cette branche de la chimie, deux aspects importants sont à prendre en compte dans
l’étude de la matière à savoir : l’aspect qualitatif et l’aspect quantitatif.
II- Aspect qualitatif de la matière:
1)- La matière :
La matière est tous corps qui possède une masse et qui occupe un volume dans l’espace. La
matière peut exister sous trois états physiques différents :
➢ L’état solide : il possède un volume et une forme définis.
➢ L’état liquide : il possède un volume définis mais aucune forme précise, il prend la
forme de son contenant.
➢ L’état gazeux : n’a ni volume ni forme définis, il prend le volume et la forme de son
contenant.
La matière peut être sous deux formes [1]:
Matière
Corps Purs
Mélange
Corps Simple
Corps Composé
Homogène
Hétérogène

Chapitre I : Préparation de solutions
11
a)- Un corps pur : il peut être soit un corps simple c'est-à-dire constitué d’une seule espèce
chimique (atome, ion ou molécule. ex : Cu, Fe, H2,O2...), soit un corps composé, c'est-à-dire
constitué de plusieurs éléments ex : l’eau pure H2O.
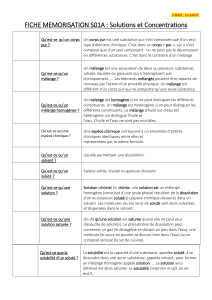
b)- Un mélange : c’est un corps constitué de plusieurs sortes d’entités chimiques mélangé
ensemble. Il existe deux types de mélanges :
➢ Les mélanges homogènes : sont des mélanges dont les constituants ne peuvent pas
être distingués à l’œil nu après agitation. (l’eau et le sel...)
➢ Les mélanges hétérogènes : sont des mélanges dont les constituants peuvent être
distingués à l’œil nu après agitation (possède deux ou plusieurs phases distinctes
exemple : l’eau et l’huile...). Un mélange hétérogène peut s’obtenir à partir de :
✓ Deux liquides : On dit alors que ces liquides ne sont pas miscibles entre
eux, tels que le liquide le moins dense est toujours au dessus de l’autre.
✓ D’un liquide et d’un solide insoluble dans ce dernier. Les particules
solides se dispersent alors dans le liquide et se déposent au fond du
récipient.
✓ D’un gaz et d’un liquide qui peuvent également constituer un mélange
hétérogène. Exemple: un soda qui libère les gaz dissous.
2)- Les solutions :
Les solutions sont un mélange homogène résultant de la dissolution d’une ou de plusieurs
substances (solutés) dans un solvant. Les molécules du soluté sont dites solvatées et elles
seront dispersées dans le solvant.
a)- Soluté : C’est toute substance à l’état pur placée dans le solvant, en quantité moins grande que
ce dernier. Ce soluté peut être solide, liquide ou gazeux.
b)- Solvant : C’est un liquide qui a la propriété de dissoudre ou de diluer d’autres substances sans
les modifier chimiquement et sans que lui-même ne soit modifié.
c)- Solutions aqueuses : Une solution ayant l’eau comme solvant est dite solution aqueuse. Il
est possible de mettre en solution :
➢ Un liquide dans un autre liquide : la solution obtenue sera limitée par la
miscibilité des deux liquides.

Chapitre I : Préparation de solutions
12
➢ un solide dans un liquide : la solution sera limitée par la solubilité du solide
dans le solvant au delà de laquelle le solide n'est plus dissous. On parle alors de
solution saturée.
➢ un gaz dans un liquide.
Il existe trois types de solutions :
➢ Solution saturée : à une température et une pression donnée, une solution
saturée est une solution qui ne peut plus dissoudre de soluté.
➢ Solution insaturée : une solution insaturée est une solution qui peut
dissoudre plus de soluté qu’elle ne contient.
➢ Solution sursaturée : une solution sursaturée est une solution contenant une
plus grande quantité de soluté dissous que celle qui correspond à la limite
de saturation.
d)- La dilution : la dilution d’une solution aqueuse consiste à en diminuer la concentration par
ajout de solvant (eau). La solution initiale de concentration supérieure est appelée solution-mère et
la solution finale de concentration inférieure est appelée solution-fille (solution diluée). Lors d’une
dilution, il ya conservation de la quantité de matière du soluté.
c)- La saturation d’une solution : c’est l’inverse de la dilution. Le solvant ne peut plus dissoudre
la totalité du soluté.
III- Aspect quantitatif de la matière:
Dans ce qui suit, nous donnons la définition de certaines propriétés pour effectuer des calculs
lors de la préparation de solutions au laboratoire :
1)- Masse molaire (M) :
La masse molaire est la masse d’une mole d’un composé chimique, elle est exprimée en
gramme par mole (g/mol).
Cette relation se traduit ainsi:
M
m
n=
n : nombre de moles ; m : masse en grammes

Chapitre I : Préparation de solutions
13
2)- Masse volumique (ρ):
La masse volumique, aussi appelée densité volumique de masse, est une grandeur physique
qui caractérise la masse d'un matériau par unité de volume. Elle est généralement notée par la
lettre grecque ρ (g/l). Elle est déterminée par le rapport :
V
m
=
avec m : la masse et V : le
volume.
3)- Densité (d):
La densité est une grandeur sans dimension et sa valeur s'exprime sans unité de mesure. La
densité d'un corps ou densité relative d'un corps est le rapport de sa masse volumique à la
masse volumique d'un corps pris comme référence. d (corps) =
)( )( réf
corps
✓ Pour les liquides et les solides, le corps de référence est l'eau pure prise à une
température de 4 °C. d (liquide) =
)( )( eau
liquide
avec ρ(eau)= 1Kg /L
✓ Dans le cas de gaz ou de vapeur, le corps de référence gazeux est l'air. La valeur de
référence prise est la masse d'un litre d'air à 0 °C sous une pression de 760 mmHg, soit
1,29349 g. d (gaz) =
)( )(air
gaz
4)- Concentration molaire ou molarité (C ou M) :
La concentration molaire d’une solution est la quantité de matière (nombre de moles) de
soluté que l’on dissous pour obtenir un litre de solution (mol/l).
La molarité varie avec la température.
5)- Concentration massique ou titre massique ou titre pondérale (t) :
C’est la masse du soluté que l’on a dissout pour obtenir un litre de solution (g/l).
C’est déterminé par la relation : t = C.M
6)- Molalité (m):
C’est le nombre de moles de soluté dans 1 Kg de solvant (mol/1kg).
Contrairement a la molarité, la molalité ne varie pas avec la température.