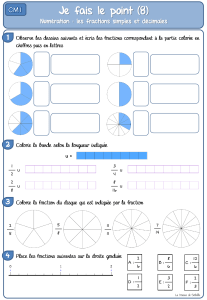
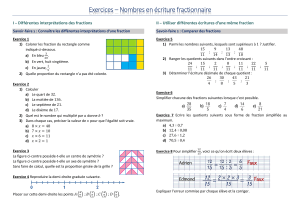
les fractions continues

UFR de Mathématique et d’Informatique
Magistère de Mathématique de Strasbourg
LES FRACTIONS CONTINUES
Mémoire de première année de Magistère
Présenté par Thomas Richez
Sous la direction de Christian Kassel, Directeur de recherche à l’IRMA
Année : 2010/2011
1

Les mathématiques ont des inventions très subtiles, et qui peuvent beaucoup servir
tant à contenter les curieux qu’à faciliter tous les arts
et diminuer le travail des hommes.
René descartes.
2

Table des matières
Introduction 5
Notations 7
1 Généralités 8
1.1 Définitions........................................ 8
1.2 Propriétés fondamentales des réduites . . . . . . . . . . . . . . . . . . . . . . . . 10
1.2.1 Théorèmes fondamentaux . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.2.2 Corollaires.................................... 12
1.3 Fractions continues à réduites positives . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3.1 Monotonie des suites des réduites dans le cas fini . . . . . . . . . . . . . . 13
1.3.2 Monotonie des suites des réduites dans le cas infini . . . . . . . . . . . . . 14
1.3.3 Autres résultats utiles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2 Fractions continues simples et rationalité 17
2.1 Premiers résultats sur les fractions continues simples . . . . . . . . . . . . . . . . 17
2.2 Algorithme de décomposition en fraction continue simple . . . . . . . . . . . . . . 20
2.2.1 Présentation de l’algorithme . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.2.2 Exemple..................................... 21
2.3 Développement en fraction continue simple finie d’un rationnel . . . . . . . . . . 22
2.4 Théorème d’approximation pour les rationnels . . . . . . . . . . . . . . . . . . . . 23
3 Fractions continues simples et irrationalité 26
3.1 Convergence des fractions continues simples infinies . . . . . . . . . . . . . . . . . 26
3.2 Développement en fraction continue simple infinie d’un irrationnel . . . . . . . . 27
3.3 Théorème d’approximation pour les irrationnels . . . . . . . . . . . . . . . . . . . 29
4 Approximation d’un irrationnel par des rationnels 31
4.1 Nombreséquivalents .................................. 31
4.2 Approximation par les réduites . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.2.1 Théorème de meilleure approximation . . . . . . . . . . . . . . . . . . . . 35
4.2.2 Un autre théorème d’approximation . . . . . . . . . . . . . . . . . . . . . 37
4.2.3 Théorème de Hurwitz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.2.4 Compléments sur les approximations d’irrationnels . . . . . . . . . . . . . 41
4.3 Fractions continues à éléments bornés et vitesse de convergence . . . . . . . . . . 41
4.3.1 Rappels de théorie de la mesure . . . . . . . . . . . . . . . . . . . . . . . . 42
4.3.2 Théorème sur les fractions continues à éléments bornés . . . . . . . . . . . 42
3

5 Fractions continues périodiques et irrationnels quadratiques 46
5.1 Généralités ....................................... 46
5.1.1 Premières définitions et premiers résultats . . . . . . . . . . . . . . . . . . 46
5.1.2 Théorème de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
5.1.3 ThéorèmedeGalois .............................. 49
5.2 Cas particulier des racines carrées . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
5.3 Equations de Pell-Fermat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
5.3.1 Recherche d’une solution particulière . . . . . . . . . . . . . . . . . . . . . 55
5.3.2 Expression des solutions positives . . . . . . . . . . . . . . . . . . . . . . . 57
5.3.3 Exemple..................................... 57
6 Compléments 59
6.1 Approche géométrique des fractions continues simples . . . . . . . . . . . . . . . 59
6.1.1 Quelques définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
6.1.2 Fractions continues et diagramme de Klein . . . . . . . . . . . . . . . . . . 59
6.2 Ordre d’approximation, nombres algébriques et transcendants . . . . . . . . . . . 62
6.3 Critère de convergence des fractions continues infinies positives . . . . . . . . . . 64
6.4 Equations diophantiennes linéaires . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Remerciements 68
Bibliographie 69
4

Introduction
Qui n’a jamais entendu parler des fractions continues ? 1Celles-ci ont été étudiées par les
plus grands mathématiciens de toute l’Histoire. On pourra citer notamment Lagrange, Galois,
Fermat, Euler, Liouville et bien d’autres encore. Aussi, la théorie des fractions continues est
déjà bien avancée et ses applications ne manquent pas. Pour vous en convaincre, il vous suffit
d’ouvrir un livre quelconque traitant de la théorie des nombres. Vous aurez alors toutes les
chances d’y découvrir une partie consacrée aux fractions continues. L’objectif de ce mémoire sera
alors d’étudier ces objets à première vue très simples mais qui recèlent bien des mystères.
La première partie constituera une introduction à cette théorie. Nous y présenterons plusieurs
résultats fondamentaux que nous utiliserons systématiquement dès la deuxième partie.
Celle-ci traitera plus particulièrement des liens existants entre les fractions continues et les
nombres rationnels. Nous verrons que tout rationnel peut être développé en une fraction continue
finie que l’on pourra qualifier de simple. Nous donnerons un algorithme permettant de développer
un rationnel en une telle fraction continue.
Puis, dans la troisième partie, nous rentrerons dans le cœur du sujet puisque nous générali-
serons certains résultats aux nombres irrationnels. Dès lors, il nous sera possible d’étudier une
application fondamentale des fractions continues, à savoir l’approximation des irrationnels par
des rationnels.
La quatrième partie sera entièrement consacrée à l’étude de telles approximations et sera no-
tamment l’occasion de répondre à la question « A quoi servent les fractions continues ? ». Nous
justifierons le fait que les fractions continues fournissent les meilleures approximations d’un irra-
tionnel par des rationnels dans un sens que nous préciserons et avec toutes les conséquences que
cela implique. Nous serons même capable de contrôler l’erreur commise dans nos approximations.
La cinquième partie traitera quant à elle d’une classe plus particulière d’irrationnels puis-
qu’il s’agira d’étudier le développement en fraction continue des nombres quadratiques dont nous
démontrerons qu’il est périodique. Nous verrons dans cette même partie une autre application
plus arithmétique des fractions continues : la résolution des équations de Pell-Fermat. Il s’agit
là d’un certain type d’équations diophantiennes non linéaires. Cette partie aura une importance
historique majeure puisque l’approximation des racines carrées et la résolution d’équations dio-
phantiennes ont été une motivation non négligeable en faveur du développement de la théorie
des fractions continues.
Enfin, l’ultime chapitre de ce mémoire apportera quelques précisions supplémentaires et no-
tamment une approche géométrique des fractions continues. La théorie de celles-ci étant un bien
vaste sujet qui mériterait nettement plus qu’un mémoire pour le recouvrir, nous ne pourrons en
présenter tous les aspects. Les approximants de Padé, du nom du mathématicien français Henri
Padé, en sont d’ailleurs de très bons exemples. Ceux-ci permettent, à l’instar des fractions conti-
1. Cette question s’adresse plutôt à un public ayant quelque peu étudié les mathématiques !
5