Primitives et intégrales

DOCUMENT 37
Primitives et int´egrales
On d´esigne par Iun intervalle de Rnon vide et non r´eduit `a un point.
1. Primitives d’une fonction
D´ efinition 37.1.On dit qu’une fonction f:I→Rpossde une primitive sur I, ou est
primitivable sur I, s’il existe une fonction F:I→Rd´erivable sur Iet telle que, pour tout
x∈I,F0(x) = f(x).Toute fonction Fd´erivable sur Iet telle que F0=fest appele une
primitive de fsur I.
On d´esignera parfois par PR(I) l’ensemble des applications de Idans Rprimitivables.
Proposition 37.1.Soit fune fonction primitivable sur I.
(1) Si Fest une primitive de fsur Ialors la fonction G:I→Rest une primitve de f
sur Isi et seulement si G−Fest constante sur I.
(2) Pour chaque x0∈Iet chaque c∈Ril existe une unique primitive Fde ftelle que
F(x0) = c.
Preuve. 1) Si G−Fest constante sur Ialors la relation G= (G−F) + Fentraine que G
est d´erivable sur Iet pour tout x∈I,
G0(x) = F0(x)+(G−F)0(x) = F0(x) = f(x).
La fonction Gest donc bien une primitive de fsur I.
R´eciproquement, si Gest une primitive de fsur Ialors, pour tout x∈I,
(G−F)0(x) = G0(x)−F0(x) = f(x)−f(x) = 0
et, I´etant un intervalle, G−Fest constante sur I.
2) Soit Fune primitive de fsur I. Pour toute primitive Gde fil existe λ∈Rtel que
G=F+λet
G(x0) = c⇔F(x0) + λ=c⇔λ=c−F(x0)
ce qui montre que G:I→Rd´efinie par G(x) = F(x)−F(x0) + cest l’unique primitive de f
prenant la valeur cen x0.
Remarque. 1). Si In’est pas un intervalle les affirmations 1.et 2.de la proposition pr´ec´edente
peuvent ˆetre fausses. Par exemple, les fonctions Fet Gde R∗dans Rd´efinies par F(x) = ln |x|,
G(x) = ln |2x|si x < 0 et G(x) = F(x) si x > 0 sont d´erivables sur R∗et, pour tout x6= 0,
F0(x) = G0(x) = 1
x.Les fonctions Fet Gsont donc des primitives sur R∗de x→1 xmais la
fonction G−Fn’est pas constante sur R∗et F(1) = G(1) = 0.
2) Toute fonction d´efinie sur In’est pas primitivable. En effet, les fonctions d´erives v´erifient
le th´eor`eme des valeurs interm´ediaires (voir le document 26). La satisfaction de ce th´eor`eme est
donc une condition n´ecessaire pour poss´eder une primitive et si f(I) n’est pas un intervalle alors
401

402 37. PRIMITIVES ET INT´ EGRALES
on est certain que fn’a pas de primitive sur I. Par exemple, la fonction partie enti`ere n’est pas
primitivable sur R.
Il existe des fonctions v´erifiant le th´eor`eme des valeurs interm´ediaires et qui ne sont pas des
fonctions d´eriv´ees. Dans le document 27, on construit une fonction d´efinie sur [0,1], satisfaisnt
ce th´eor`eme et continue en aucun point. Cette fonction n’est pas une d´eriv´ee car si une d´eriv´ee
est d´efinie sur un intervalle alors l’ensemble des points o`u elle est continue est dense dans son
intervalle de d´efinition (Document 26).
3) Il existe des fonctions primitivables non continues et mˆeme non born´ees au voisinage d’un
point. Par exemple, soit f:R→Rd´efinie par
F(x) = x2sin 1
x2si x6= 0 et F(0) = 0.
Cette fonction est d´erivable sur Ret
F0(x) = 2xsin 1
x2−2 xcos 1 x2si x6= 0 et F0(0) = 0.
La fonction f=F0est primitivable sur Ret n’est born´ee sur aucun voisinage de 0.
4) On d´esigne par Zf(x)dx l’ensemble des primitives de fmais ce symbole d´esigne parfois
une primitive de fd’o`u une certaine ambiguit´e de cette notation.
Proposition 37.2.Pour tout intervalle I,PR(I)est un espace vectoriel sur R.
Preuve ´evidente.
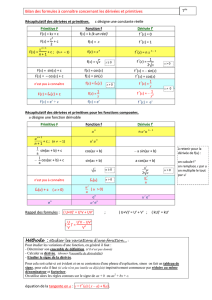
Ce r´esultat permet de trouver des primitives par combinaison lin´eaire de fonctions ´el´ementaires
primitivables. On obtient ces derni`eres fonctions en lisant de droite `a gauche un tableau don-
nant les d´eriv´ees usuelles. Par exemple une primitive sur R∗de x→2 sin x+ 3 1
x+ 4 est
x→ −2 cos x+ 3 ln |x|+ 4xet toute fonction polynˆome est primitivable.
Remarque. Si PR(I) est bien un sous espace vectoriel de l’espace vectoriel des fonctions
d´efinies sur I, en revanche ce n’est pas une sous alg`ebre. En d’autres termes, un produit de
fonctions d´eriv´ees n’est pas n´ecessairement une fonction d´eriv´ee.
Exemple. Soit fet gde Rdans Rd´efinies par f(0) = g(0) = 0 et, pour x6= 0, f(x) = x2sin 1
x,
g(x) = x2cos 1
x. Les fonctions fet gsont d´erivables sur Ravec f0(0) = g0(0) = 0 et, pour
x6= 0, f0(x) = 2xsin 1
x+ cos 1 x,g0(x) = 2xcos 1 x−sin 1 x. Si h:R→Rest d´efinie par
h(x) = f0(x)2+g0(x)2−4x2alors h(0) = 0 et h(x) = 1 pour x6= 0. Cette fonction hn’est donc
pas primitivable et donc au moins l’une des fonctions (sans doute les deux) (f0)2ou (g0)2n’est
pas une fonction d´eriv´ee.
2. Primitives et int´egrale d’une fonction continue
2.1. D´efinition et propri´et´es. Nous avons vu que toute fonction admettant une primitive
sur un intervalle v´erifie le th´eor`eme des valeurs interm´ediaires et l’on sait que ce th´eor`eme est
satisfait par les fonctions continues. Nous admettrons le th´eor`eme suivant dont diff´erentes
preuves seront vues dans la partie ”Compl´ements ” de ce document.
Th´ eor` eme 37.1.Toute fonction continue sur un intervalle Ipossde des primitives sur I.

2. PRIMITIVES ET INT´ EGRALE D’UNE FONCTION CONTINUE 403
Lemme 37.1.Soit fune fonction primitivable sur Iet aet bdeux ´el´ements de cet intervalle.
Le nombre rel F(b)−F(a)est ind´ependant de la primitive Fde f.
Preuve. C’est une cons´equence imm´ediate de la proposition 37.1
D´ efinition 37.2.Soit fune fonction ayant une primitive Fsur Iet a,b∈I. Le nombre
r´eel F(b)−F(a)est appel´e int´egrale entre aet bde fet on note
F(b)−F(a) = Zb
a
f(x)dx .
Remarques. 1) Dans la notation Zb
a
f(x)dx la variable xest muette et peut ˆetre remplac´ee
par toute autre variable sans occurrence dans f. On a par exemple Zb
a
f(x)dx =Zb
a
f(t)dt =
Zb
a
f(u)du.
2) Il r´esulte imm´ediatement de la d´efinition que Za
a
f(x)dx = 0 et Zb
a
f(x)dx =−Za
b
f(x)dx.
Proposition 37.3.Soit fune fonction ayant une primitive Fsur Iet a∈I. La fonction
Gde Idans Rd´efinie par
G(x) = Zx
a
f(t)dt
est d´erivable sur Iet est la primitive de fprenant la valeur 0 au point a.
Preuve. On a G(x) = F(x)−F(a) d’o`u la d´erivabilit´e de Gsur Iavec G0(x) = F0(x) = f(x).
De plus G(a) = F(a)−F(a) = 0.
Remarque. Si on remplace la notion d’int´egrale introduite ici par celle d’int´egrale de Riemann
alors on est certain que Gest d´erivable en x0∈Iseulement si fest continue en x0et on a alors
G0(x0) = f(x0). Par exemple la fonction partie enti`ere de xest int´egrable au sens de Riemann
sur Rmais x→Zx
0
E(t)dt est seulement d´erivable sur R−Zet cette fonction n’est donc pas
une primitive de la fonction partie enti`ere (qui n’est pas primitivable sur R).
Dans la suite, nous allons ´etudier les propri´et´es de l’int´egrale d’une fonction con-
tinue mais de nombreux r´esultats s’´etendent facilement au cas des fonctions primitivables. On
d´esignera par C0(I, R) l’espace vectoriel r´eel des fonctions continues sur I.
Proposition 37.4.(La relation de Chasles) Soit a,bet ctrois ´el´ements de Iet fune
fonction continue sur I. On a
Zb
a
f(x)dx =Zc
a
f(x)dx +Zb
c
f(x)dx.
Preuve. Soit Fune primitive de fsur I. L’´egalit´e cherch´ee est une autre fa¸con d’´ecrire
F(b)−F(a) = F(b)−F(c) + F(c)−F(a).

404 37. PRIMITIVES ET INT´ EGRALES
Proposition 37.5.(Lin´earit´e de l’int´egrale) Soit fet gdeux fonctions continues sur I.
Pour tout (λ, µ)∈R2et tout (a, b)∈I2
Zb
a
(λf(x) + µg(x))dx =λZb
a
f(x)dx +µZb
a
g(x)dx.
Preuve. On utilise la d´efinition de l’int´egrale et le fait que si Fet Gsont des primitives de
fet gsur Ialors λF +µG est une primitive de λf +µg.
Proposition 37.6.(Positivit´e de l’int´egrale) Soit fune fonction continue et positive sur
I= [a, b]. Si a < b alors Zb
a
f(x)dx ≥0et Zb
a
f(x)dx = 0 si et seulement si fest identiquement
nulle sur [a, b].
Preuve. Soit Fune primitive de fsur I. Comme la fonction fest positive, Fest croissante
et a < b implique F(a)≤F(b) d’o`u Zb
a
f(x)dx ≥0.
Si Zb
a
f(x)dx = 0 alors F(a) = F(b) et la fonction F´etant croissante, elle est constante sur
[a, b] et sa d´eriv´ee fest identiquement nulle. La r´eciproque est ´evidente.
Remarques. 1) La proposition est encore vraie si fn’est pas continue. Si on consid`ere
l’int´egrale au sens de Riemann, la premi`ere affirmation de la proposition est toujours vraie mais
la seconde peut ˆetre fausse si fn’est pas continue. Par exemple, Z1
0
E(x)dx = 0 et la fonction
partie enti`ere n’est pas identiquement nulle sur [0,1]. Cependant, si on consid´ere l’int´egrale de
Riemann d’une fonction ayant une primitive alors on peut faire la mˆeme d´emonstration qu’ici
et le r´esultat est donc vrai.
2) On peut r´esumer les deux propositions pr´ec´edentes en disant que f→Zb
a
f(x)dx est une
forme lin´eaire positive sur C0(I, R).
Corollaire 37.1.Soit fet gdeux fonctions continues sur I= [a, b]. Si pour tout x∈[a, b],
f(x)≤g(x)alors Zb
a
f(x)dx ≤Zb
a
g(x)dx,
l’in´egalit´e stricte ayant lieu si et seulement si il existe x0∈[a, b]tel que f(x0)< g(x0).
Preuve. Il suffit d’appliquer la proposition 37.6 `a la fonction continue et positive h=g−f.
Corollaire 37.2.L’application
(f, g)∈ C0(I, R)2→ hf|gi=Zb
a
f(x)g(x)dx
est un produit scalaire sur C0(I, R).
Peuve. En utilisant la proposition 37.5 on voit que (f, g)→ hf|giest une forme bilin´eaire
qui est ´evidemment sym´etrique. La proposition 37.6 entraine qu’elle est de plus d´efinie positive.

2. PRIMITIVES ET INT´ EGRALE D’UNE FONCTION CONTINUE 405
Remarque. On peut d´eduire du corollaire pr´ec´edent l’in´egalit´e de Cauchy-Schwarz qui est
v´erifi´ee par toute forme bilin´eaire sym´etrique et positive :
Si fet gsont continue sur [a, b] alors
|Zb
a
f(x)g(x)dx| ≤ (Zb
a
f(x)2dx)1
2(Zb
a
g(x)2dx)1
2,
l’´egalit´e ayant lieu si et seulement si il existe λ∈Rtel que f=λg.
On d´eduit de ce r´esultat un cas particulier (p=q=1
2) de l’in´egalit´e de Minkowski
(Zb
a
(f(x) + g(x))2dx)1
2≤(Zb
a
f(x)2dx)1
2+ (Zb
a
g(x)2dx)1
2.
(Pour la preuve, partir de (f+g)2=f2+g2+ 2fg.)
Une preuve directe de l’in´egalit´e de Cauchy-Schwarz se trouve dans le document du fascicule
1 consacr´e au trinˆome du second degr´e.
Corollaire 37.3.(L’in´egalit´e des accroissements finis) Soit fune fonction d´erivable sur
[a, b]avec a < b. S’il existe (m, M)∈R2tel que
m≤f0(x)≤M
alors
m(b−a)≤f(b)−f(a)≤M(b−a).
Preuve. Il suffit d’appliquer le corollaire 37.1.
Exercice. Etudier la suite (In) d´efinie pour n > 0 par
In=Zπ
2
0
(sin x)1
ndx.
Si x∈[0,π
2] alors 0 ≤sin x≤1 et 0 ≤(sin x)1
n≤(sin x)1
n+1 ≤1. Le corollaire 37.1 entraine
que 0 ≤In≤In+1 ≤π
2. La suite croissante et major´ee Inest donc convergente.
On a 2
πx≤sin x(voir Document 33) d’o`u ( 2 πx)1
n≤(sin x)1 net donc
Zπ
2
0
(2
πx)1
ndx ≤In.
Une primitive sur [0,π
2] de x→(2 πx)1
nest ( 2
π)1
nn
n+ 1xn+1
net
Zπ
2
0
(2
πx)1
ndx = ( 2
π)1
nn
n+ 1(π 2)n+1
n=n
n+ 1
π
2
d’o`u n
n+ 1
π
2≤In≤π 2et lim
n→∞ In=π
2.
Remarques. 1). Attention ! La preuve de la proposition 37.6 utilise le fait qu’une fonction
ayant une d´eriv´ee positive sur un intervalle est croissante sur cet intervalle. La preuve tr`es
´el´ementaire de l’in´egalit´e des accroissements finis donn´ee ici suppose donc aussi ce r´esultat alors
que souvent il est d´emontr´e en utilisant l’´egalit´e ou l’in´egalit´e des accroissements finis. On peut