TP Cours : Polarisation rectiligne de la lumière

TP#Cours#:#Polarisation#
rectiligne#de#la#lumière#
#
Les$ondes$lumineuses$sont$des$ondes$électromagnétiques$vectorielles.$Certains$systèmes$physiques,$
comme$ par$ exemple$ les$ lunettes$ de$ soleil$ polarisantes,$sont$ sensibles$ à$ la$ nature$ vectorielle$ de$ la$
lumière,$c’est?à?dire$à$la$polarisation-de-la-lumière.$Le$but$de$ce$TP?Cours$est$de$définir$ce$qu’est$la$
polarisation$ de$ lumière$ et$ d’étudier$ des$ dispositifs$ permettant$ de$ produire$ et$ d’analyser$ la$
polarisation$des$ondes$lumineuses$dans$le$cas$particulier$de$la$polarisation$rectiligne.$
1. La%polarisation%des%ondes%lumineuses%
1.1. %Nature%vectorielle%des%ondes%lumineuses%
Dans$ le$ premier$ chapitre$ d’optique,$ nous$ avons$ vu$ que$ la$ lumière$ est$ une$ onde$(ou$ champ)$
électromagnétique,$dont$la$longueur$d’onde$pour$la$lumière$visible$est$comprise$dans$le$domaine$:$
400!nm!≤!!≤750!nm$
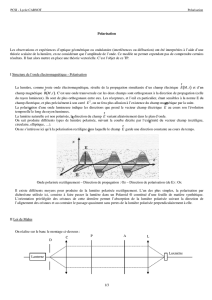
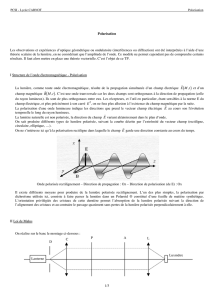
Tout$ état$ du$ champ$ électromagnétique$peut$ se$ décomposer$ sur$ une$ base$ d’ondes$ planes$
progressives$sinusoïdales,$correspondant$la$propagation$couplée$d’un$champ$électrique$et$d’un$champ$
magnétique,$perpendiculaires$$entre$eux$et$perpendiculaires$à$la$direction$de$propagation$de$l’énergie$
lumineuse.$ Les$ champs$ électrique$ et$ magnétique$ sont$ contenus$ dans$ le$ plan- d’onde,$ plan$
perpendiculaire$à$la$direction$de$propagation$du$champ$électromagnétique.$
$
$
Définition$:$
La$ polarisation- de- la- lumière$est$ par$ définition$ l’évolution$ de$ la$ direction$ du$ vecteur$ champ$
électrique$au$cours$du$temps.$
$

2################################ # # #TP#O2#:#Polarisation#rectiligne#de#la#lumière#
1.2. %Etats%de%polarisation%des%ondes%lumineuses%
•-Lumière-polarisée-ou-non-polarisée-
On$ dit$ que$ la$ lumière$ est$ totalement- polarisée- lorsqu’en$ chaque$ point$ la$ direction$ du$ champ$
électrique$est$bien$définie,$c’est?à?dire$qu’elle$ne$varie$pas$aléatoirement$au$cours$du$temps.$Dans$le$
cas$contraire,$on$dit$que$la$lumière$n’est$pas$polarisée$ou$non-polarisée.$
La$lumière$fournie$par$les$lampes$à$incandescence$est$non$polarisée,$de$même$que$celle$fournie$par$
les$lampes$spectrales.$Certains$lasers$fournissent$quant$à$eux$une$lumière$totalement$polarisée.$
•-Etats-de-polarisation-d’une-lumière-totalement-polarisée-
La$polarisation$totale$de$la$lumière$peut$être$de$trois$sortes$:$
? polarisation- rectiligne$ou$ polarisation- linéaire-:$ la$ direction$ du$ champ$ électrique$ est$
constante$au$cours$du$temps$et$de$la$propagation$
? polarisation-circulaire-:$la$ direction$du$champ$ électrique$tourne$au$cours$du$temps$mais$son$
amplitude$reste$constante$
? polarisation-elliptique-:$la$direction$du$ champ$électrique$tourne$au$cours$du$temps$ avec$ une$
amplitude$non$constante-
-
Une$polarisation$circulaire$ou$elliptique$est$qualifiée$de$droite$$lorsqu’on$la$voit$tourner$dans$le$sens-
horaire$(donc$vers$la$droite)$lorsqu’elle$nous$vient$$dans$l’œil.$
Au$ contraire,$une$polarisation$ circulaire$ ou$ elliptique$ est$ qualifiée$ de$ gauche$$lorsqu’on$ la$ voit$
tourner$dans$le$sens-trigonométrique$(donc$vers$la$gauche)$lorsqu’elle$nous$vient$$dans$l’œil.$
Nous$n’aborderons$dans$ce$TP$que$le$cas$de$la$polarisation$rectiligne.$

#TP#O2#:#Polarisation#rectiligne#de#la#lumière############### ## #######3#
2. Production%d’une%lumière%polarisée%rectilignement%
Pour$obtenir$une$onde$ polarisée$dans$un$ état$ donné,$ et$à$ défaut$ de$ source$polarisée,$on$utilise$un$
polariseur,$ c’est?à?dire$ un$ dispositif$ susceptible$ d’agir$ soit$ sur$ la$ lumière$ naturelle,$ soit$ sur$ de$ la$
lumière$dans$ un$ état$ de$ polarisation$ différent.$ Les$ polariseurs$ les$ plus$ utilisés$ sont$ les$ polariseurs-
rectilignes,$qui$permettent$de$transformer$la$lumière$incidente$en$lumière$polarisée$rectilignement.$
2.1. %Polarisation%par%dichroïsme%
•-Principe-du-polariseur-dichroïque-
Le$ dichroïsme$ correspond$ à$ l’absorption$ sélective$ de$ la$ lumière$ en$ fonction$ de$ sa$ direction$ de$
polarisation.$Il$est$à$la$base$du$polariseur$rectiligne$le$plus$couramment$utilisé$à$l’heure$actuelle$:$le$
polaroïd1-ou$polariseur-dichroïque.$
Un$polariseur$dichroïque$se$ présente$ sous$ la$ forme$ d’une$ feuille$ en$ matière$ plastique$ de$ quelques$
dixièmes$de$millimètres$d’épaisseur,$généralement$de$teinte$gris$neutre.$Cette$feuille$est$constituée$de$
longues$ chaînes$ de$ polymères$ étirées$ majoritairement$ dans$une$ direction.$ Le$ polariseur$ dichroïque$
absorbe$la$lumière$lorsque$celle?ci$est$polarisée$selon$la$direction$de$l’axe$des$chaînes$de$polymères$
(excitation$des$ états$ vibrationnels$maximal),$mais$presque$ pas$ lorsque$celle?ci$ est$ polarisée$selon$la$
direction$ perpendiculaire$ à$ l’axe$ des$ chaînes$ de$ polymères$ (excitation$ des$ états$ vibrationnels$
minimal),$ appelée$ axe- passant$du$ polariseur.$ De$ cette$ façon,$ l’absorption$ du$ polariseur$ dichroïque$
dépend$très$fortement$de$la$direction$de$polarisation.$
Remarque$:$ les$ polymères$ n’interagissent$ plus$ avec$ la$ lumière$ si$ la$ longueur$ d’onde$ de$ celle?ci$ est$
trop$loin$d’une$transition$électronique,$ce$qui$explique$le$très$mauvais$fonctionnement$des$polaroïds$
dans$l’infrarouge.$
•-Action-d’un-polariseur-dichroïque-sur-une-onde-non-polarisée-
Expérience$:$Plaçons$un$polariseur$dichroïque$entre$une$lampe$blanche$et$un$écran.$
On$ constate$ que$ l’intensité$ lumineuse$ sur$ l’écran$ n’est$ pas$ modifiée$ lorsqu’on$ fait$ tourner$ le$
polariseur$dans$le$plan$perpendiculaire$à$la$direction$de$propagation$de$l’onde$lumineuse.$
Interprétation$:$La$lumière$provenant$de$la$lampe$étant$non$polarisée,$la$direction$du$polariseur$ne$
modifie$ en$ rien$ les$ observations$ faites$ à$ l’écran$ puisqu’il$ n’y$ a$ pas$ de$ direction$ privilégiée$ dans$ la$
lumière$ incidente.$Par$ contre,$en$ sortie$ du$ polariseur$ rectiligne,$ la$ lumière$ est$ désormais$ polarisée$
rectilignement$selon$la$direction$de$l’axe$passant$du$polariseur.$
$
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1$Polaroïd$est$une$marque$déposée$par$la$Polaroïd$Corporation,$Cambridge,$Massachusetts,$USA$

4################################ # # #TP#O2#:#Polarisation#rectiligne#de#la#lumière#
•-Action-d’un-polariseur-dichroïque-sur-une-onde-polarisée-rectilignement-:-loi-de-Malus-
Expérience$:$En$laissant$le$premier$polariseur$dichroïque$P1$en$place,$plaçons$un$second$polariseur$
P2$dichroïque$sur$le$trajet$du$faisceau.$
Lorsqu’on$ fait$ tourner$ P2,$ on$ constate$ que$ l’intensité$ lumineuse$ sur$ l’écran$ est$ modulée.$ Plus$
précisément,$l’intensité$lumineuse$passe$par$deux$maxima$et$ deux$extinctions$lorsqu’on$fait$ un$ tour$
complet$(360°)$avec$P2.$En$faisant$tourner$P1$au$lieu$de$P2,$on$observe$exactement$la$même$chose.$
Interprétation$:$Le$polariseur$dichroïque$P1$sert$de$polariseur,$c’est?à?dire$qu’il$permet$d’obtenir$en$
sortie$une$polarisation$rectiligne$selon$l’axe$passant$de$P1.$Le$second$polariseur$P2$sert$d’analyseur,$
c’est?à?dire$qu’il$ne$laisse$quant$à$lui$passer$que$la$projection$de$la$polarisation$issu$de$P1$selon$son$
axe$passant$:$ainsi$la$lumière$sur$l’écran$est$maximale$lorsque$les$axes$passants$des$deux$polariseurs$
sont$ parallèles$ et$ minimale$ (extinction)$ lorsque$ les$ axes$ passants$ des$ deux$ polariseurs$ sont$
perpendiculaires.$
$
Loi$ de$ Malus$:$ La$ loi$ de$ Malus$ donne$ l’intensité$ transmise$ par$ un$ polariseur$ lorsque$ celui?ci$ est$
éclairé$ par$ une$ onde$ lumineuse$ d’intensité$ !!,$ de$ polarisation$ rectiligne$ faisant$ un$ angle$ !$avec$ la$
direction$de$l’axe$passant$du$polariseur$:$
!!!=!!cos!!$
!"#$%&'()'*+*,-%*.'*/0()*123#4&5-'6*0..-7'%*.0*.07#'*/.0()8'*'4*#.0)'%*-(*#%'7&'%*#3.0%&9'-%6*(34$*:;6*
9-%* .'* 4%0<'4* 1'* .0* .-7&=%'>* ?$%&@&'%* %0#&1'7'(4* 5-'* .2&(4'(9&4$* 4%0(97&9'* #0%* :;* ('* A0%&'* #09* .3%95-23(*
43-%('*:;*B#-&95-'*.0*.07#'*/.0()8'*@3-%(&4*-('*.-7&=%'*(04-%'..'C>*
:.0)'%*0.3%9*-(*9')3(1* #3.0%&9'-%6*(34$* :D6*'(4%'* .'*#%'7&'%* #3.0%&9'-%* '4* .2$)%0(>*E'#$%'%*93(* 0"'* 1'*
#3.0%&904&3(*'(*%'#$%0(4*.2'"4&()4&3(*+*.20(F.'*'(4%'*.'9*0"'9*#0990(49*'94*0.3%9*1'*!=90°>*

#TP#O2#:#Polarisation#rectiligne#de#la#lumière############### ## #######5#
G* .20&1'* 12-(*.-"7=4%'* B)2'94HIH1&%'* -(* 7'9-%'-%* 1'* #-&990()'* .-7&('-9'C6* 7'9-%'%* 0.3%9* .0* #-&990()'*
4%0(97&9'*#0%*.'*9J94=7'*'(*@3()4&3(*1'*.20(F.'*!*'(4%'*.'9*0"'9*#0990(49*1'9*1'-"*#3.0%&9'-%9>*E'#%'(1%'*
.2'"#$%&'()'*#%$)$1'(4'*'(*#.0K0(4*-(*@&.4%'*A'%4*#-&9*-(*@&.4%'*%3-F'*0A0(4*.'*#%'7&'%*#3.0%&9'-%>*
!$
90°$
80°$
70°$
60°$
50°$
40°$
30°$
20°$
10°$
0°$
!!" %
$
$
$
$
$
$
$
$
$
$
!!"#$ !" %
$
$
$
$
$
$
$
$
$
$
!!"#$% !" $
$
$
$
$
$
$
$
$
$
$
?$%&@&'%*0.3%9*.0*A0.&1&4$*1'*.0*.3&*1'*L0.-9>*
2.2. %Polarisation%par%réflexion%vitreuse%
L’observation$ d’une$ scène$ quotidienne$ à$ travers$ un$ polaroïd$ permet$ de$ se$ rendre$ compte$ qu’une$
quantité$importante$de$la$lumière$naturelle$(non$polarisée)$est$polarisée$par$réflexion$sur$des$surfaces$
lisses$diélectriques,$c’est?à?dire$non$métalliques$(par$exemple$vitres,$peintures,$matières$plastiques,$
surfaces$des$liquides…).$Si$on$observe$soigneusement,$on$constate$que$cette$polarisation$est$partielle$
(on$ ne$ parvient$ pas$ à$ obtenir$ une$ extinction$ complète$ comme$ c’était$ le$ cas$ dans$ l’expérience$
précédente),$rectiligne$selon$la$direction$parallèle$à$la$surface.$
Expérience$:$Envoyons$un$faisceau$issu$d’une$diode$laser$verte$non$polarisée$(le$vérifier$au$préalable$
à$l’aide$d’un$polariseur$dichroïque)$sur$un$milieu$homogène$diélectrique$(verre$ou$plastique).$D’après$
les$lois$de$Snell?Descartes,$le$rayon$incident$donne$naissance$à$un$rayon$réfléchi$et$à$un$rayon$réfracté.$
Nous$nous$intéressons$ici$à$la$polarisation$de$la$lumière$réfléchie.$On$place$pour$cela$un$polariseur$
dichroïque$ entre$ le$ rayon$ réfléchi$ et$ l’écran$ et$ on$ observe$ l’intensité$ transmise$ en$ fonction$ de$
l’orientation$ du$ polariseur$ dichroïque,$ qui$ nous$ sert$ ici$ d’analyseur.$On$ constate$ alors$ une$ nette$
modulation$de$l’intensité$transmise,$avec,$dans$le$cas$général,$passage$par$un$minimum$non$nul.$
On$peut$à$présent$faire$varier$l’angle$d’incidence$sur$le$milieu$homogène$(angle$!!)$et$on$constate$que$
pour$une$ incidence$particulière,$appelée$incidence- de- Brewster$ou$ angle-de- Brewster,$ on$ obtient$
une$extinction$totale$avec$l’analyseur.$
Interprétation$:$ L’expérience$ précédente$ nous$ permet$ d’affirmer$ que$ la$ lumière$ réfléchie$ est$
polarisée$rectilignement$alors$que$la$lumière$incidente$n’était$pas$polarisée$:$il$y$a$donc$phénomène$de$
polarisation-par-réflexion.$
Cette$ polarisation$ par$ réflexion$ est$ totale$ pour$ un$ angle$ d’incidence$ particulier,$ appelé$ angle- de-
Brewster,$correspondant$à$un$angle$droit$entre$le$rayon$réfléchi$et$le$rayon$transmis.$
$