Leçon – Traceur graphique de mouvement uniforme unidimensionnel

Physique 1 de 11
© 2006 Alberta Education <www.learnalberta.ca>
Leçon – Traceur graphique de
mouvement uniforme unidimensionnel
L’applet Traceur graphique de mouvement uniforme unidimensionnel t’apprendra
comment construire et utiliser des graphiques position-temps et vitesse
vectorielle-temps en vue d’étudier le mouvement unidimensionnel.
Préalables
Cette leçon te permettra de t’exercer à construire et à utiliser des graphiques position-
temps et vitesse vectorielle-temps en vue d’étudier le mouvement unidimensionnel.
L’applet devrait être ouvert. Les directives présentées dans le texte qui suit doivent être
exécutées dans l’applet. Il pourrait être nécessaire d’alterner entre les instructions et
l’applet si l’espace écran est limité. Tu devrais être prêt à faire des calculs pour vérifier
les nombres générés par l’applet. Si tu as besoin d’aide en utilisant l’applet, consulte
l’option Aide – Constructeur de mouvement uniforme unidimensionnel.
Contenu
• Utilisation de graphiques position-temps et vitesse vectorielle-temps pour
représenter le mouvement unidimensionnel
• Relation entre la pente d’un graphique position-temps et la vitesse vectorielle
• Relation graphique entre l’aire sous la pente d’un graphique vitesse vectorielle-
temps et le déplacement
• Résolution de problèmes complexes à l’aide de l’applet Constructeur de
mouvement unidimensionnel
L’utilisation de graphiques position-temps et vitesse vectorielle-temps pour
représenter le mouvement uniforme unidimensionnel
Les graphiques sont des instruments visuels puissants qui permettent de comprendre
de nombreuses notions de physique. Savoir construire des graphiques position-temps
et vitesse vectorielle-temps et les comprendre est une habileté qu’il est important que tu
acquières. Étudie les graphiques qui suivent et donne une brève description du
mouvement semblable à celle de l’exemple ci-dessous :

Physique 2 de 11
© 2006 Alberta Education <www.learnalberta.ca>
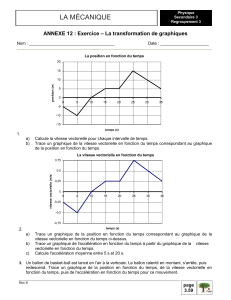
1. Exemple : Une élève fai
t du jogging le long
d’un sentier en ligne droite. Le graphique
de droite montre sa position (mesurée à
partir de son point de départ) en fonction
du temps. Réponds aux questions
suivantes :
a) Quelle est sa position la plus
éloignée de son point de départ
et à quel moment cela a-t-elle eu
lieu?
(Réponse : L’examen du
graphique montre que la plus
grande distance par rapport au
point de départ est 19 m et que
cela a eu lieu au temps t = 5 s.)
b) Quelle est la différence entre son
mouvement de
0 s à 5 s (points A et C) et son
mouvement de 5 s à 7 s (C à D)?
(Réponse : De A à C, son
déplacement
par rapport au point
de départ devient plus grand.
Après cela, son déplacement par
rapport au point de départ
commence à diminuer. Elle doit
avoir fait demi-tour et revenir
maintenant sur ses pas.)
c) Durant quelle partie du
mouvement se déplaçait-elle le
plus rapidement? Explique ta
réponse.
(Réponse : Du point C au
point D, elle a parcouru (19 m -
7 m) = 12 m en un total de (7 s -
5 s) = 2 s. Sa vitesse vectorielle
était de (12 m)/(2 s) = +6 m/s.
Cette vitesse vectorielle est plus
grande que pour n’importe quelle
autre section du graphique.)

Physique 3 de 11
© 2006 Alberta Education <www.learnalberta.ca>
2. Un élève pressé de se rendre au cours
de physique saute dans sa voiture et
« met la pédale au fond »! Le graphique
de droite montre la position de sa
voiture en fonction du temps.
a) Détermine le déplacement de la
voiture au cours des 5 premières
secondes?
b) À quel moment la voiture a-t-elle
atteint sa plus grande vitesse
vectorielle? Comment peux-tu
l’expliquer en examinant
simplement le graphique (pas de
calcul)?
c) Calcule la plus grande vitesse
vectorielle atteinte par la voiture
au cours des 7 secondes
représentées sur le graphique.
d) Quelle était la vitesse vectorielle
moyenne de la voiture durant
l’intervalle de 7 secondes?
Souviens-toi que la vitesse
vectorielle moyenne est définie
par :

Physique 4 de 11
© 2006 Alberta Education <www.learnalberta.ca>
3. La figure de droite montre le
graphique vitesse vectorielle-temps
pour une voiture de course
téléguidée.
a) Quelle est la vitesse vectorielle
la plus grande atteinte par la
voiture? Quand cela se
passe-t-il?
b) Quelle est la vitesse vectorielle
la plus basse? (Attention, il y a
deux réponses!) Q
uand cela se
produit-il?
c) Peux-tu dire jusqu’à quelle
distance la voiture s’est
éloignée simplement en
examinant le graphique?
d) Le graphique montre quatre
« phases » distinctes dans le
mouvement. Remplis le
tableau ci-dessous, puis entre
les données dans l’applet
Constructeur de mouvement
uniforme unidimensionnel pour
construire un graphique et
insère-le à droite.
Intervalle de temps (s) Vitesse vectorielle
(m/s)
0 - 1 ______
1 - 2 ______
2 - 3 ______
3 - 7 ______

Physique 5 de 11
© 2006 Alberta Education <www.learnalberta.ca>
4. Le graphique vitesse vectorielle-
temps tracé pour un objet est illustré à
droite.
a) À quelle vitesse vectorielle se
déplaçait l’objet entre
t = 3 secondes et
t = 5 secondes?
Détermine son
déplacement durant cet
intervalle.
b) Comment pourrais-tu
déterminer le déplacement de
l’objet au cours des sept
secondes entières
représentées ici?
c) Il existe trois phases distinctes
dans le mouvement représenté
ici. Détermine ces phases et
remplis le tableau ci-dessous.
Utilise cette information et
l’applet Constructeur de
mouvement uniforme
unidimensionnel pour
construire un graphique et
insère-le à droite :
Intervalles de temps (s) Vitesse vectorielle
(m/s)
_____ ______
_____ ______
_____ ______