Télécharger le fichier - Les math en secondaire 1 avec Mme

Panorama 4
Unité 4.3
 Les droites perpendiculaires
 Définition et notation
 Construction à l’aide de l’équerre
 Construction à l’aide du rapporteur d’angle
1
Placer la ligne de foi sur la droite ou le segment et
aligner le 90° avec le point par lequel on désire
que notre droite perpendiculaire passe.
2
Tracer une petite marque vis-à-vis 90°.
3
Enlever le rapporteur d’angle. Avec la règle,
tracer la droite qui passera par le point A et la
petite marque. Ajouter un petit carré qui signifiera
que les droites sont perpendiculaires.

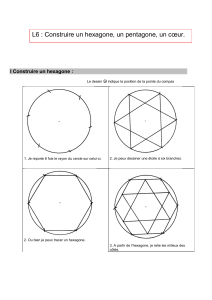
 Construction à l’aide du compas (NE PAS UTILISER LES DEUX POINTS QUI SONT
SUR LA DROITE)
1
Placer la pointe sèche du compas sur le
point extérieur et tracer un arc de cercle
qui coupera la droite en deux endroits pas
trop rapprochés.
2
Conserver la même ouverture et aller
tracer un arc de cercle en plaçant la pointe
sèche sur chacun des croisements entre
la droite et le premier arc de cercle.
3
Avec la règle, tracer la droite qui passe
par le point A et le nouveau point B.
Ajouter un petit carré qui signifiera que les
droites sont perpendiculaires.
o Exemples : Voir Feuille 11 verso

 La Réflexion
 Définition : la réflexion est un retournement d’une figure par rapport à un axe.
 ATTENTION : Il faut faire la différence entre la réflexion (symétrie orthogonale) et la
symétrie centrale (rotation de 180°).
Symétrie orthogonale (RÉFLEXION)
Symétrie centrale (ROTATION de 180°)

 Figure invariante : Certaines figures sont leur propre image par une réflexion. La figure
est alors dite invariante ou symétrique à elle-même et l’axe de réflexion est appelé axe
de symétrie. Une telle figure peut avoir plus d’un axe de symétrie.
 Effectuer une réflexion :
o Exemples : Voir Feuille 15

 La médiatrice
 Définition
La médiatrice est une droite perpendiculaire à un segment passant par son milieu. La
médiatrice coupe donc le segment en deux parties isométriques.
 Dans un triangle, les trois médiatrices se rencontrent en un point, le centre du cercle
circonscrit.
 Construction à l’aide de l’équerre et du rapporteur d’angle
Trouver d’abord le milieu du segment et ensuite faire tout simplement une
perpendiculaire comme vu précédemment.
 Construction à l’aide du compas
1
Placer la pointe sèche du compas sur le
point A et l’ouvrir plus grand que la moitié
de la longueur du segment AB. Tracer un
arc de cercle.
2
Conserver la même ouverture et aller
tracer un arc de cercle en plaçant la pointe
sèche sur le point B.