Synthèse : démonstration en géométrie

Ch 4 : démonstration – synthèse JA
Synthèse : démonstration en géométrie
Sujet Reims – 1995
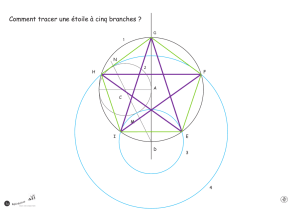
1. a) reproduire la figure suivante à l’aide de la règle non graduée et du compas, à partir du
segment [AB] donné.
b) Ecrire un programme de construction en utilisant le vocabulaire de la géométrie du cycle 3 de
l’école primaire et permettant à un élève de ce cycle n’ayant pas vu la figure, de la réaliser à partir
d’un segment [AB] donné.
c) montrer que les côtés du pentagone ABEGF ont la même longueur. Cela prouve-t-il qu’il est
régulier ? Pourquoi ?
d) quelle est la nature précise des quadrilatères ABSC et ABDS ? Justifiez vos réponses.
e) Montrer que les points C, S, D sont alignés.
f) comment compléter CABD de façon à faire apparaître un hexagone régulier ? Justifier.
NB : si ABCDE… est un polygone régulier de n côtés et si O est le centre du cercle circonscrit alors
les angles au centre mesure 360 / n.
Figure à reproduire.

Ch 4 : démonstration – synthèse JA
Correction : démonstration en géométrie
Sujet Reims – 1995
1. b) Le segment [AB] est donné :
- tracer le cercle C1 de centre B et de rayon AB
- tracer le cercle C2 de centre A et de rayon AB
- ces cercles se coupent en R et S (S en dessous de [AB])
- tracer la droite (RS)
- tracer le cercle C3 de centre S et de rayon SA = AB
- ce cercle coupe C1 en D, C2 en C et [RS] en O, au dessus de [AB]
- tracer la droite (DO), elle coupe le cercle C2 en F (
][ODF 
)
- tracer la droite (CO), elle coupe le cercle C1 en E (
][OCE 
)
- tracer un arc de cercle de centre F et de rayon AB, puis un arc de cercle de centre E et de rayon
AB. Ils se coupent en G au-dessus de R.
- tracer les segments : [BE], [EG] ; [GF] ; [FA]
c) par construction AF = AB = FG = GE = EB puisque rayons de cercles égaux.
Il faut maintenant prouver que les angles sont égaux à 360 : 5 = 72°
d) ABSC et ABDS sont des losanges
en effet AB = BS comme rayons de C1
SC = BS comme rayons de C3 AB = BS = SC = AC d’où losange
AC = AB comme rayons de C2
De même pour ABDS
e) on sait que AS = BS = AB (question d) le triangle ASB est équilatéral.
(RS) est l’axe de symétrie de la figure composée par les deux cerclesC1 et C2.
Donc ASO = OSB = 30°
AC = CS = AS (question d), le triangle ACS est équilatéral, CSA = 60°
CSO = CSA + ASO = 60+30 = 90°
De la même manière OSD = 90°. On peut donc écrire que CSD = CSO + OSD = 180°.
Ce qui prouve que les points C, S, D sont alignés.
f) Les 3 triangles CSA, ASB et BSD forment la moitié d’un hexagone inscrit dans le cercle C3. Il
suffit alors de construire, à l’aide du compas, les points P et Q sur ce cercle de manière à ce que
BD= DP et AC = CQ.

Ch 4 : démonstration – synthèse JA